Álgebra de distribuciones

Las distribuciones matemáticas son potentes y útiles para modelar muchas situaciones de negocios, especialmente aquellas en las que hay incertidumbre. Envision trata las distribuciones como ciudadanos de primera clase y puede gestionar una amplia gama de operaciones que deben realizarse con estas mismas distribuciones. Todas estas operaciones se conocen en conjunto como el álgebra de distribuciones, que Envision admite. En esta sección, presentaremos este tipo de datos de distribución y veremos los diferentes operadores y las diferentes funciones que pueden aplicarse a él.

El tipo de datos de distribución    Trazado de una distribución    Operaciones puntuales ( pointwise )    Generación de distribuciones    Ampliación de una distribución a una tabla    Convolución de distribuciones de probabilidades    Desarrollos históricos

El tipo de datos de distribución

Las distribuciones matemáticas son objetos que generalizan la noción de funciones. En Envision, nuestra ambición es más modesta, y lo que llamamos distribuciones son en realidad funciones $f: \mathbb{Z} \to \mathbb{R}$. Llamamos a estas funciones (matemáticas) distribuciones porque el caso de uso más frecuente en Envision es el de gestionar distribuciones de probabilidad, es decir, distribuciones estrictamente positivas que tienen una masa igual a 1.

En Envision, las distribuciones se materializan a través de un tipo de datos especial llamado distribución. Otros tipos de datos incluyen número o texto. El tipo de dato de distribución muestra comportamientos relativamente complejos, precisamente porque es una función en lugar de un valor individual. Por ejemplo, a continuación generamos una Dirac, es decir, una función discreta con un valor 0 en todas partes, con excepción del punto 42, donde tiene un valor 1.

d := dirac(42)

Las distribuciones pueden exportarse en un archivo utilizando los archivos de datos de Ionic. Sin embargo, las distribuciones no pueden exportarse tal cual en archivos CSV o de Excel.

Envision ofrece muchas otras maneras de generar distribuciones que veremos en las secciones a continuación.

Trazado de una distribución

Las distribuciones pueden visualizarse en histogramas. Consideremos una simple distribución de Poisson:



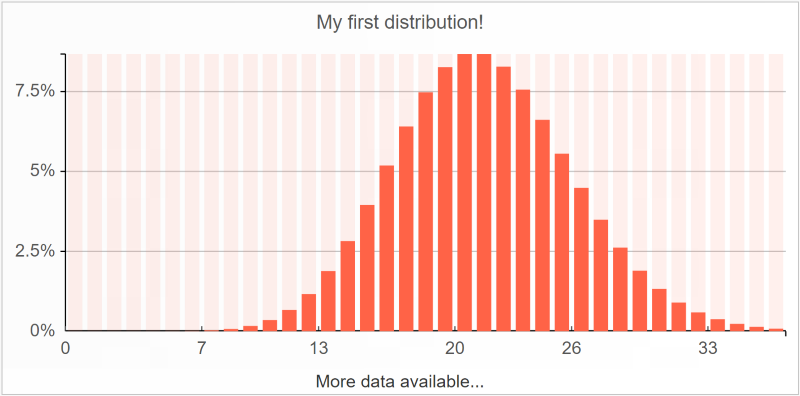
Este trazado se ha generado en Envision con una script de una sola línea que se detalla a continuación:

show histogram "My first distribution!" tomato with 
poisson(21)

El mosaico histogram espera que se proporcione una distribución única escalar después de la palabra clave with.

Operaciones puntuales (pointwise)

Las operaciones más simples en distribuciones se conocen como operaciones puntuales (pointwise). Por ejemplo, supongamos que $f$ y $g$ representan dos distribuciones $\mathbb{Z} \to \mathbb{R}$. Luego, podemos definir la suma como:

$$f+g: k \to f(k) + g(k)$$ Desde la perspectiva de Envision, suponiendo que tanto X como Y son vectores de distribución, la misma operación puede escribirse de modo similar de esta manera:

Z = X + Y

Es preciso señalar que incluso cuando se trabaja con distribuciones, Envision sigue siendo un lenguaje vectorial. Por lo tanto, generalmente no se procesa una sola distribución a la vez, sino un vector de distribución completo. La misma operación puede realizarse desde una perspectiva escalar utilizando lo siguiente:

Z := X + Y

En esta sección y en las siguientes, cada vez que utilizamos X e Y en ejemplos de script, suponemos que estas dos variables son distribuciones reales.

Luego, la multiplicación y la resta puntuales se definen del siguiente modo: $$f \times g: k \to f(k) \times g(k)$$ $$f-g: k \to f(k)-g(k)$$ que se traduce de modo bastante transparente en la siguiente sintaxis de Envision:

Z = X * Y
Z = Z - Y

Desde la perspectiva de que un número $\alpha$ puede asimilarse implícitamente en una función constante $f_{\alpha}: k \to \alpha$, Envision permite la combinación de números y distribuciones, pero solo si la distribución resultante es compacta.

// OK, es compacta
Z = 2 * X 
// OK porque no divide por 0
Z = X / 2 
// incorrecta, no es una distribución compacta
Z = X +1 
// incorrecta, Y es compacta, por lo tanto, tiene valores iguales a cero
Z = X/Y

Las distribuciones también pueden desplazarse. El operador de desplazamiento generalmente se escribe del siguiente modo:

$$f_{n}: k \to f(k+n)$$ La sintaxis correspondiente de Envision es:

Z = X << n // desplazamiento hacia la izquierda
Z = X >> n // desplazamiento hacia la derecha

Naturalmente, si n es negativo, los operadores de desplazamiento siguen trabajando, pero el desplazamiento hacia la izquierda se vuelve un desplazamiento hacia la derecha, y viceversa.

Generación de distribuciones

Existen varias maneras de crear distribuciones. El motor de pronóstico de Lokad genera distribuciones para tiempos de entrega o demanda futuros. Cuando estas distribuciones han sido serializadas en forma de grilla (*), es posible regenerar la distribución a través de la función distrib(). La sintaxis es la siguiente:

Demand = distrib(Id, G.Probability, G.Min, G.Max)

La variable Demand resultante es una distribución. Cuando la grilla original incluye segmentos que son más largos que 1, distrib() distribuye la masa de manera uniforme a lo largo del segmento. La función distrib() es la que preserva la masa de la distribución.


Además, Envision ofrece la posibilidad de generar una distribución directamente desde un conjunto de valores numéricos observados. Esta es la finalidad del agregador ranvar():

X = ranvar(Orders.Quantity)

El agregador ranvar() devuelve una variable aleatoria que corresponde a la frecuencia observada en los grupos de agregación. Cuando no hay nada que agregar, ranvar() devuelve dirac(0).

Por último, es posible generar una distribución a partir de una serie de tiempo, utilizando el agregador ranvar.segment().

D = ranvar.segment(
// primera fecha para cada artículo
start: Items.Start 
// última fecha (inclusiva) para cada artículo
end: Items.End 
// longitud del período para cada artículo
horizon: Items.Horizon 
// entero para omisión de elementos
step: Items.Step 
// la fecha de cada evento
date: Orders.Date 
// la cantidad de cada evento
quantity: Orders.Quantity) 

Calcula, para cada artículo, la distribución de la suma de cantidades de eventos para períodos de longitud de horizonte completos entre la primera y la última fecha de ese artículo. Generalmente, el horizonte debería ser el tiempo de entrega de un artículo.

Ampliación de una distribución a una tabla

En la sección anterior, hemos visto cómo se puede agregar una tabla a una distribución. El proceso inverso, es decir, la ampliación de una distribución en líneas de tabla, también es posible. En esta sección veremos la función extend.distrib(), que hace precisamente esto. La sintaxis se ilustra a continuación:

X = poisson(1)
table G = extend.distrib(X)
G.Probability = int(X, G.Min, G.Max)
show table "My Grid" with
Id
G.Min
G.Max
G.Probability

Donde X es el vector de distribución generado en la línea 1 como una distribución de Poisson. En la línea 2, las distribuciones se introducen en una tabla denominada G (de grilla). Esta tabla tiene un (Id, *) afín y, como se ilustra entre las líneas 3 y 7, se autorrellena con las columnas numéricas G.Min y G.Max. Tanto G.Min como G.Max son límites inclusivos.

Cuando se amplían distribuciones relativamente compactas, la tabla resultante generalmente contiene líneas de incrementos +1, es decir G.Min y G.Max aumentadas de a 1 de una línea a la siguiente. Sin embargo, si consideráramos la ampliación de distribuciones de altos valores, por ejemplo dirac(1000000), sería extremadamente ineficiente generar millones de líneas. Por lo tanto, la función extend.distrib() agregará grandes distribuciones en cubos más grandes. Esto explica por qué tenemos tanto a G.Min como a G.Max, que representan límites inclusivos del cubo.

Para poder tener más control sobre la granularidad de los cubos generados, la función extend.distrib() ofrece la primera sobrecarga:

table G = extend.distrib(X, S)

Donde S es un vector numeral. La tabla resultante proporciona cubos alineados con los segmentos [0;0] [1;S] [S+1; S+M] [S+M+1;S+2*M] ... donde M es la dimensión de cubo predeterminada, también llamada multiplicador. Esta sobrecarga es típica de cuando debe considerarse la demanda por sobre el stock total.

Por último, la segunda sobrecarga de extend.distrib() proporciona aún más control con:

table G = extend.distrib(X, S, M)

donde M es una dimensión de cubo obligatoria. Si M es cero, la ampliación invierte la dimensión de cubo predeterminada, ajustada automáticamente por Envision. Esta segunda sobrecarga es particularmente útil cuando hay multiplicadores de lote en el proceso de pedido, ya que la demanda debe lotearse en cubos de una dimensión específica.

Tenga en cuenta que extend.distrib(X, S, M) puede fallar dependiendo de la capacidad asignada a su cuenta de Lokad si intenta ampliar una distribución de alto valor forzando un multiplicador bajo.

Convolución de distribuciones de probabilidades

Las convoluciones representan una clase de operaciones más avanzadas sobre las distribuciones. Los casos de uso principales de las convoluciones implican variables aleatorias. A diferencia de las operaciones puntuales, las convoluciones tienen interpretaciones probabilísticas, como la suma o la multiplicación de variables aleatorias independientes. Es posible reconocer las convoluciones en Envision por sus operadores de dos caracteres que terminan en *, a saber:

// convolución aditiva
Z = X +* Y 
// convolución de sustracción, igual que X +* reflect(Y)
Z= X -* Y
// convolución multiplicativa
Z = X ** Y 
// potencia de convolución
Z = X ^* Y 

La convolución aditiva (o la de sustracción) puede interpretarse como la suma (o la diferencia) de dos variables aleatorias independientes $X+Y$ (o $X-Y$). La convolución multiplicativa, también conocida como convolución de Dirichlet, puede interpretarse como el producto de dos variables aleatorias independientes.

La potencia de convolución es más compleja y representa: $$X ^ Y = \sum_{k=0}^{\infty} X^k \mathbf{P}[Y=k] \text{ where } X^k = X + \dots + X \text{ ($n$ times)}$$ Esta operación es de interés por su relación con el proceso que lleva a un pronóstico de demanda integrada, donde $X$ representa la demanda diaria —que se supone es estacionaria— e $Y$ representa los tiempos de entrega probabilísticos.

Vea también nuestra página sobre la potencia de convolución.

Desarrollos históricos

El motor de pronóstico de Lokad comenzó a ofrecer grillas de cuantiles a principios de 2015. Estas grillas aún no eran exactamente distribuciones de probabilidad —eran simplemente pronósticos cuantílicos interpolados—, pero nos estábamos acercando bastante. Trabajando con nuestros clientes, comenzamos a darnos cuenta del enorme potencial que tenía la aplicación del análisis probabilístico a la optimización de la cadena de suministro cuantitativa. Sin embargo, nuestras grillas eran solo eso: grandes tablas que enumeraban todas las probabilidades. Y a medida que estas grillas se convirtieron en un avance tanto para nuestros clientes como para nosotros mismos, nos dimos cuenta de que las probabilidades de procesamiento representadas en forma de listas no eran una tarea fácil.

El álgebra de las distribuciones representa una respuesta tecnológica amplia de Lokad a los desafíos de la cadena de suministro que involucran futuros desconocidos. De hecho, esas situaciones no requieren solo un único pronóstico de mediana, sino un análisis completo de los riesgos de todas las posibilidades. Envision adopta la idea de que deberían considerar todos los escenarios y no concentrarse solo en un puñado de ellos. Para esta finalidad, es posible introducir variables aleatorias en los scripts de Envision y manipularlas a través de operaciones específicamente adaptadas para ellas, como las convoluciones. Se darán más detalles al respecto a continuación. En la práctica, el álgebra de las distribuciones es una manera elegante de modelar situaciones de cadena de suministro complejas en las que tanto la demanda como el tiempo de entrega futuros son inciertos.