di Joannès Vermorel, ultima modifica: Settembre 2011In logistica, si dice che la domanda (o le vendite) di un certo prodotto
è soggetta a stagionalità quando la serie temporale corrispondente presenta una variazione ciclica prevedibile, che dipende dal periodo dell'anno. La stagionalità è uno dei pattern statistici usati più comunemente per affinare la precisione delle previsioni della domanda.
Esempio: molti rivenditori occidentali registrano un picco di vendite nel periodo di Natale.
Serie temporali stagionali: illustrazione
Nel grafico qui sotto vediamo
4 serie temporali stagionali (cliccare per ingrandire). Le serie temporali sono aggregate a livello settimanale su un periodo di 159 settimane (circa 3 anni). I dati rappresentano le consegne settimanali di 4 diversi prodotti che partono dal magazzino di un grande rivenditore europeo.
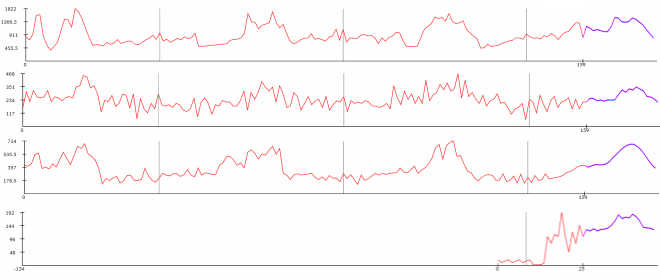
Il primo giorno dell'anno (1° gennaio) è indicato da un segno grigio verticale. I dati storici sono in rosso, mentre le previsioni di Lokad sono in viola. La stagionalità può essere vista come un insieme di pattern che si ripetono in modo simile da un anno all'altro, con segni grigi verticali che fungono da riferimento.
Decomposizione stagionale: un modello di base
Sia
Y(t) la domanda nel momento
t. Decomponiamo la domanda
Y(t) in due componenti:
S(t), funzione strettamente ciclica, e
Z(t), il complemento non stagionale. Si ha:
Y(t) = S(t) * Z(t) dove
S(t + 1 anno) = S(t)Se partiamo dal presupposto che possiamo calcolare la funzione
S(t), allora il processo di previsione si svolgerà in tre fasi.
- Calcolare le serie temporali destagionalizzate
Z(t) = Y(t) / S(t). - Produrre una previsione per le serie temporali Z(t), eventualmente attraverso la media mobile.
- Riapplicare in seguito gli indicatori di stagionalità alla previsione.
Per tornare al problema iniziale, e cioè stimare gli indicatori stagionali
S(t), supponendo che non ci sia un trend (tra le altre cose),
S(t) può essere stimata come:
S(t) = MEDIA( Y(t-1)/MA(t-1) + Y(t-2)/MA(t-2) + Y(t-3)/MA(t-3) + ... )dove
Y(t-1) è la forma abbreviata di
Y(t - 1 year) e
MA(t) la media mobile a 1 anno su
Y(t).
L'approccio che proponiamo in questa sezione è piuttosto
ingenuo, ma può essere facilmente implementato in Excel. Esistono, tuttavia, in letteratura, molti modelli statistici che affrontano la stagionalità con metodi ben più complicati (Box-Jenkins, ARMA, ARIMA, Holt-Winters...).
Stima degli indicatori stagionali: sfide e problemi
Il modello stagionale che abbiamo appena illustrato è piuttosto semplicistico e funziona soprattutto con le serie temporali stagionali lunghe e regolari. In realtà, esistono molte difficoltà pratiche nel calcolo della stagionalità:
- le serie temporali sono brevi. Il ciclo di vita della maggior parte dei beni di consumo non supera i 3 o 4 anni. Di conseguenza, lo storico delle vendite di un prodotto offre, in media, pochissimi punti nel passato utili a stimare ogni indicatore stagionale (ossia i valori di S(t) nel corso dell'anno, cfr. sezione precedente);
- le serie temporali contengono rumore. Le fluttuazioni casuali del mercato influiscono sulle vendite e rendono la stagionalità più difficile da isolare;
- bisogna tener conto di più stagionalità. Se consideriamo le vendite a livello di punto vendita, la stagionalità del prodotto è strettamente connessa alla stagionalità del punto vendita stesso;
- altri pattern, come il trend o il ciclo di vita del prodotto, influiscono sulle serie temporali, introducendo bias di ogni sorta nella stima della stagionalità.
Un metodo semplice per aggirare questi ostacoli, ma che richiede molta manodopera, consiste nel creare manualmente dei
profili di stagionalità, a partire da aggregati di prodotti noti per avere tutti lo stesso comportamento stagionale. Il ciclo di vita di un aggregato di prodotti normalmente è molto più lungo del ciclo di vita di un singolo prodotto, il che mitiga gli effetti dei problemi appena descritti.
Quasi-stagionalità
Molti pattern si ripresentano una volta l'anno, ma
non sempre alla stessa data. Noi di Lokad definiamo questi pattern come
quasi-stagionali. Ad esempio, la Festa della Mamma (che cade in date diverse ogni anno e in ogni Paese) e altre festività, come il Ramadan, la Pasqua e Hanukkah (che ogni anno cadono in giorni diversi) sono quasi-stagionali.
Gli
eventi quasi-stagionali sfuggono ai modelli classici di previsione ciclica, poiché questi partono dal presupposto che la ciclicità sia costante. Per gestire la quasi-stagionalità, abbiamo bisogno, quindi, di una logica più complessa, "quasi-ciclica", appunto.
Cosa propone Lokad
Per esperienza, sappiamo che
la stagionalità condiziona gran parte delle attività umane. In particolare, nelle serie temporali che rappresentano la vendita di beni di consumo (prodotti sia food che non food), la stagionalità è quasi onnipresente. Tuttavia, succede spesso che, a causa del rumore prodotto dal mercato, la stima degli indicatori stagionali finisca per essere di qualità così bassa da essere praticamente inutilizzabile nel perfezionamento delle previsioni.
La
tecnologia di previsione di Lokad è pensata appositamente per gestire sia la stagionalità che la quasi-stagionalità: non sarà necessario
suggerire a Lokad di tenerne conto, ci abbiamo già pensato noi.
Abbiamo visto quali sfide pone il fatto che molte serie temporali, sia nel settore retail che nel settore produzione, contengano un numero esiguo di dati storici. Per ovviare al problema, Lokad ricorre a una
analisi a serie temporali multiple: in questo caso, la stagionalità viene valutata non su un singolo prodotto, ma su un gruppo di prodotti. In questo modo, non solo riduciamo il rumore nella stima della stagionalità, ma consentiamo anche di introdurre la stagionalità nelle previsioni per prodotti sul mercato da meno di un anno.
