di Joannès Vermorel, Febbraio 2012La funzione di perdita pinball, chiamata anche perdita di quantile, è un indicatore utilizzato per valutare l'accuratezza di una previsione quantilica.
Valutare
l'accuratezza di una
previsione quantilica è una sfida, perché, contrariamente alle previsioni tradizionali, dove l'obiettivo è che la previsione sia il più possibile vicina ai valori osservati, le previsioni quantiliche si basano su una situazione in cui viene introdotto di proposito un errore sistematico, o
bias. Sarebbe quindi troppo semplicistico confrontare la
situazione osservata con le
previsioni. La
funzione di perdita pinball restituisce dei valori che possono essere interpretati come un indice
dell'accuratezza di un modello di previsione quantilica.
Formula
Sia $\tau$ il quantile desiderato, $y$ il valore reale e $z$ la previsione quantilica. Allora $L_\tau$, la funzione di perdita pinball, potrà essere scritta come segue:
$$
\begin{eqnarray}
L_{\tau}(y,z) & = & (y - z) \tau & \textrm{ if } y \geq z \\\
& = & (z - y) (1 - \tau) & \textrm{ if } z > y
\end{eqnarray}
$$
Scarica: pinball-loss-function.xlsxIl foglio di calcolo mostra come calcolare la funzione di perdita pinball con Microsoft Excel. La formula vera e propria non è molto più complicata di altri indicatori di accuratezza, come il MAPE.
Illustrazione
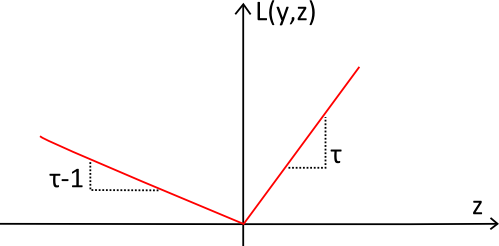
La funzione di perdita pinball (in rosso) è chiamata così per via della sua forma, che ricorda la traiettoria della pallina di un
flipper (pinball in inglese). La funzione è sempre positiva. Più ci allontaniamo da $y$, maggiore sarà il valore di $L_\tau(y,z)$.
L'inclinazione è usata per riflettere lo
squilibrio desiderato nella previsione quantilica.
I migliori modelli quantilici hanno una bassa perdita pinball
Il risultato più importante associato alla funzione di perdita pinball è che
più è bassa la perdita pinball, più accurata è la previsione.
Possiamo provare che il quantile ottimale può essere ottenuto anche con la funzione che minimizza la perdita pinball. Tuttavia, la dimostrazione richiederebbe un livello di formalismo ben al di là dello scopo di questo articolo.
Pertanto, per confrontare l'accuratezza di due diversi modelli di previsione (ad esempio, il modello di Lokad contro quello di un altro sistema), è sufficiente calcolare la perdita pinball
media in ogni modello, su un insieme di serie temporali abbastanza grande da assicurarci che la differenza osservata sia statisticamente rilevante - qualche centinaio di serie temporali basteranno a stabilire quale dei modelli sia il più
accurato.
Cosa propone Lokad
A nostro giudizio, la presunta
semplicità del concetto di accuratezza per le previsioni tradizionali (medie, quindi) è piuttosto sopravvalutata. Le previsioni, che siano medie o quantiliche, sono soggette al fenomeno dell'overfitting, che complica significativamente il confronto tra diversi modelli di previsione. La funzione di perdita pinball costituisce, però, un modo molto semplice per valutare l'accuratezza
relativa di due modelli di previsione quantilica.
Leggi anche
- Sequential Quantile Prediction of Time Series, marzo 2011, di Gerard Biau e Benoit Patra, Information Theory, IEEE Transactions
- Continuous Ranked Probability Score (CRPS), una generalizzazione della funzione di perdita pinball per le previsioni probabilistiche
