di Joannès Vermorel, Febbraio 2012La regressione quantilica è un particolare tipo di regressione (ossia di previsione), che introduce
di proposito un bias, o errore sistematico, nel risultato. Invece che cercare la
media della variabile da prevedere, la regressione quantilica cerca la
mediana e altri quantili (chiamati a volte
percentili). I quantili sono molto
utili nell'ottimizzazione delle scorte come metodo diretto per calcolare il
punto di riordino.
Regressione è qui usato come sinonimo di previsione. Il termine "regressione" fa riferimento all'approccio matematico, mentre "previsione" fa riferimento all'uso pratico del risultato.
Il concetto di regressione quantilica è un argomento di statistica relativamente avanzato. Scopo di questo articolo sarà non di trattare l'argomento in modo rigoroso, ma di fornire un'introduzione (relativamente) intuitiva per i professionisti del retail e dell'industria manifatturiera.
Illustrazione visiva dei quantili
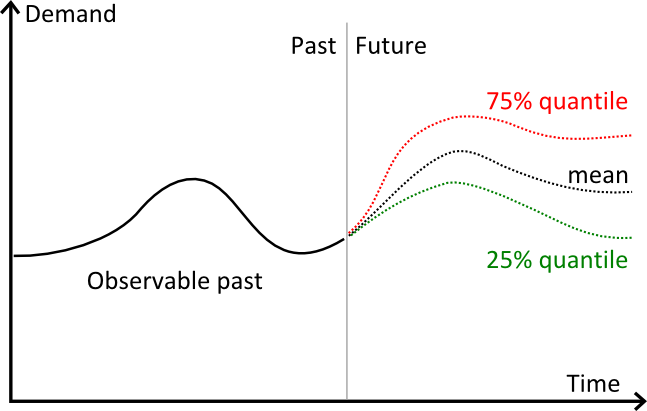
Il grafico illustra 3 diverse previsioni:
- in rosso, una previsione quantilica al 75%;
- in nero, una previsione media;
- in verde, una previsione quantilica al 25%.
Visivamente, i quantili si comportano come degli intervalli di confidenza. Nella pratica, però, il quantile serve solo per ottenere una singola percentuale desiderata.
Quantili (o percentili) della domanda futura
Il tipo di previsione più tradizionale e più intuitivo è la
previsione media: il
peso rispettivo di una sovraprevisione e di una sottoprevisione devono equivalersi, altrimenti nella previsione verrebbe introdotto un
bias, o errore sistematico (più precisamente, un
bias rispetto alla media).
Sebbene l'assenza di un bias sia auspicabile, non è per forza indice di accuratezza. Una previsione, anzi, può non contenere un bias ed essere comunque inesatta. Il bias indica soltanto la propensione di un modello di previsione a sovrastimare o sottostimare il futuro.
Una versione perfezionata di questo tipo di previsione è la
previsione mediana: la
frequenza di sovraprevisioni e sottoprevisione deve equivalersi, altrimenti la previsione conterrà un
bias rispetto alla mediana.
A questo punto, abbiamo già modificato il concetto di previsione senza
bias, passando da
pesi uguali a
probabilità uguali. Si tratta di una piccola modifica, che però potrebbe avere un impatto numerico significativo, almeno in alcuni casi.
Esempio: reddito familiare medio e mediano negli USA
Il
reddito familiare illustra la profonda differenza tra media e mediana.
Secondo l'Ufficio per il censimento degli Stati Uniti, nel 2004, il reddito familiare mediano era di 44.389 dollari USA, mentre il reddito medio era di 60.528 dollari USA, cioè più alto di quasi il 40% rispetto a quello mediano.
Questa discrepanza è possibile perché i redditi delle famiglie americane più ricche sono relativamente elevati rispetto a quelli del resto della popolazione. Il divario tra media e mediana si ritrova in tutte le distribuzioni non simmetriche, ossia tutte quelle che non seguono una distribuzione normale.
Generalizzazione della mediana
La mediana è la soglia al livello della quale la distribuzione si divide in probabilità di 50/50. Tuttavia, è possibile considerare anche
altre percentuali di frequenza, come ad esempio 80/20 o 90/10, o qualsiasi altro rapporto che abbia come somma 100%.
I quantili rappresentano una
generalizzazione della mediana a una data percentuale. Per τ, un valore tra 0 e 1, la regressione quantilica Q(τ) rappresenta la soglia al livello della quale la probabilità di osservare un valore inferiore alla soglia è pari esattamente a τ.
Previsioni quantiliche
Sia le previsioni tradizionali, sia le previsioni quantiliche sono elaborate a partire dalle
serie temporali, che quindi costituiscono i dati di input. Oltre ai dati, una previsione tradizionale
media di serie temporali richiede altri due parametri extrastrutturali:
- il periodo, ossia giorno, settimana o mese;
- l'orizzonte, un numero intero che indica i periodi da prevedere.
Implicitamente, le serie temporali sono aggregate secondo il
periodo, mentre l'orizzonte è un qualsiasi orizzonte sufficientemente ampio da poter essere di uso pratico, solitamente maggiore del
lead time.
Le previsioni
medie hanno un vantaggio considerevole: è
matematicamente corretto sommare le previsioni. Ad esempio, se
y1,
y2,
y3 e
y4 rappresentano le 4 settimane precedenti la previsione, e se vogliamo prevedere la domanda
solo delle prossime
due settimane, allora possiamo sommare
y1+y2.
Al contrario,
sommare le previsioni quantiliche non è matematicamente corretto, o, più precisamente, la somma dei quantili non dà il quantile della somma (somma dei segmenti).
Vediamo perché i quantili non possono essere sommati. Poniamo che un giocatore d'azzardo giochi una moneta da €1 a settimana a una slot machine. Poniamo che le probabilità di vincita siano dell'1% per un premio da €50 e zero nel resto dei casi. Se consideriamo il quantile 99% del premio previsto, avremo un premio settimanale di €50 ogni settimana. Se invece consideriamo il quantile 99% per due settimane, il premio previsto sarà sempre di €50. Infatti, la probabilità di vincere due volte è solo dello 0,01% (1% moltiplicato per 1%), quindi il quantile 99% rimarrà invariato. Se sommiamo i due quantili 99% settimanali, abbiamo come risultato €100, ma, in realtà, sappiamo che ci vorranno 16 settimane per accumulare un guadagno di €100 per il quantile 99% (non pubblichiamo la dimostrazione matematica, poiché andrebbe oltre lo scopo di questo articolo).
Poiché le previsioni quantiliche non possono essere sommate, per elaborare previsioni con serie temporali quantiliche dobbiamo
riconsiderare il concetto stesso dell'aggregazione temporale. Infatti, produrre previsioni quantiliche
per periodo è un'operazione discutibile, dato che questo tipo di previsioni
elementari non possono essere combinate per produrre dei quantili corretti sui segmenti.
In questo modo, la previsione
quantilica delle serie temporali presenta una struttura distinta:
- τ è il quantile previsto, espresso in percentuale;
- λ è l' orizzonte, che esprime una durata (di solito in giorni).
Ad esempio, se le serie temporali indicano le vendite del prodotto A, e se abbiamo τ=0,90 e λ=14 giorni, allora la previsione quantilica (τ, λ) darà come risultato un valore della domanda che abbia esattamente il 90% di possibilità di essere superiore alla domanda totale osservata in 14 giorni (e, di riflesso, il 10% di probabilità di essere inferiore alla domanda in quegli stessi 14 giorni).
A differenza delle previsioni tradizionali, le previsioni quantiliche producono
uno e un solo valore per serie temporale, indipendentemente dall'orizzonte. In certa misura, le previsioni quantiliche sono più
agnostiche rispetto al periodo, in confronto alla loro controparte tradizionale.
Cosa propone Lokad
A prima vista, le previsioni quantiliche potrebbero sembrare più complicate rispetto a quelle tradizionali. Ciò nonostante, in molte situazioni reali, i professionisti del settore finiscono per elaborare previsioni
medie, per poi
estrapolarle subito come previsioni quantiliche, partendo dal presupposto che le previsioni seguano una distribuzione normale. Tuttavia, durante l'estrapolazione si corre il rischio di degradare notevolmente il risultato finale della previsione. In realtà, sarebbe la tecnologia di previsione a doversi adattare alle esigenze della vita pratica, producendo direttamente previsioni quantiliche, e non il contrario.
Leggi anche
- Punto di riordino, su come applicare i quantili all'ottimizzazione delle scorte.
- Funzione di perdita pinball, su come misurare l'accuratezza di una previsione quantilica.
- Roger Koenker, Kevin F. Hallock, (2001) Quantile Regression, Journal of Economic Perspectives, 15 (4), 143–156.
- Ichiro Takeuchi, Quoc V. Le, Timothy D. Sears, Alexander J. Smola, (2006), Nonparametric Quantile Estimation, Journal of Machine Learning Research 7 1231–1264.
