分位数回归（时序）

首页 » 知识库 » 此处
作者：Joannes Vermorel，2012 年 1 月

回归类型（即预测）有意在结果中引入了偏差。分位数回归着眼于所预测变量的平均数，而非着眼于中位数以及其他任何分位数（有时称为百分位数）。作为一种直接计算再订货点的方法，分位数对于库存优化尤其有用。


分位数回归的概念是相对较高级的统计主题，本文的目的并非探讨该主题的严谨处理，而在于为零售业或制造业的从业者就该主题提供（相对）直观的介绍。

分位数示例

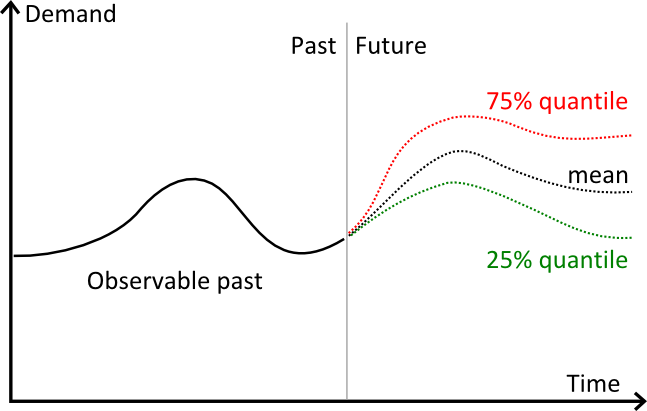
上图说明了 3 种不同预测：

• 红色部分为 75% 分位数预测。
• 黑色为平均数预测。
• 绿色部分为 25% 分位数预测。
  

从视觉上说，分位数的行为与置信区间非常类似。但在实践中，只有单一的目标百分比才需要分位数。

未来需求的分位数（或百分位数）

平均数预测为典型预测，这种预测也是最直观的预测：过高预测与过低预测相应的权重应相等，否则预测就会出现偏差（更准确地说是偏向平均数）。


针对这一愿景的第一步精进便是中位数预测：过高预测与过低预测相应的频率应相等，否则预测将偏向于中位数。

在这一点上，无偏差预测的概念已从相等权重转变为相等机会。这种转变看似细微，但在某些情况下，对数值的影响非常大。

示例：美国家庭收入的平均数与中位数的对比

家庭收入诠释了平均数和中位数之间的巨大差异。


之所以出现这种情况，是因为美国富人家庭的收入明显高于其余人群。所有非对称的分布（通常是所有不遵循正态分布的分布）的平均数和中位数之间都会存在这样的差异。

中位数的泛化

中位数表示将分布按 50/50 分割的阈值。但是，也可以考虑其他频率比。例如，我们可以考虑 80/20、90/10 或者其他任何总百分比值仍为 100% 的比率。

分位数表示中位数对指定百分比值的泛化。例如 τ，其值介于 0 和 1 之间，分位数回归 Q(τ) 表示观察到值低于阈值的几率正好为 τ 的位置处的阈值。

分位数预测

无论是典型预测还是分位数预测，都是以时序作为输入。时序表示输入数据。除了数据，典型的平均数时序预测还需要进行另外两项结构设置：

• 周期，例如天、周或月。
• 水平线，表示所要预测周期数的整数值。
  

时序根据周期隐式聚合，所选水平线的范围应具有实用性，通常要大于交付周期。

平均数预测具有一项非常便利的属性：对预测之和执行正确运算。举个例子，如果 y1、y2、 y3 和 y4 表示向前预测 4 周，那么如果我们只需要对接下来两周的需求进行预测，那么可以对 y1+y2 求和。

但是，分位数预测求和无法执行正确运算，或者更准确地说，分位数之和不能生成和（各部分之和）的分位数。



由于分位数预测不能求和，所以分位数时序预测需要重新考量周期聚合的基本概念。实际上，生成按周期的分位数预测有争议，因为这些基础预测无法通过组合来对各个部分生成正确的分位数。

基于此，分位数时序预测采用了不同的结构：

• τ，即目标分位数，为一个百分比值。
• λ，即水平线，表示持续时间（通常用天表示）。
  

举个例子，如果时序表示产品 A 的销售情况，并且 τ=0.90，λ=14 天，则分位数预测 (τ, λ) 将返回大于 14 天内观察到的总需求的几率正好为 90% 时的需求值（小于相同 14 天内需求的几率则为 10%）。

与典型预测相反，分位数预测将独立于水平线生成一个时序，并且每个时序仅有一个值。在一定程度上，分位数预测比典型预测更具周期不可知性。

Lokad 特性

乍看之下，分位数预测似乎比典型预测更复杂。然而在很多实际情况中，实践者常止于生成第一个平均数预测，然后便直接将它们作为分位数预测进行外推，并且通常假设这些预测遵循正态分布。但是，外推操作常常表示整个流程中最弱的一个环节，可能明显降低最终结果的质量。预测技术应顺应实践要求，即提供原生的分位数预测，而不是提供其他途径。

参考资料

• 再订货点，了解分位数如何应用于库存优化。
• Pinball 损失函数，了解如何度量分位数预测的准确性。
• Roger Koenker，Kevin F. Hallock，(2001) 分位数回归，Journal of Economic Perspectives，15 (4), 143–156
• Ichiro Takeuchi，Quoc V. Le，Timothy D. Sears，Alexander J. Smola，(2006)，非参数方法估计分位数，Journal of Machine Learning Research 7 1231–1264