Algebra der Verteilungen

Startseite » Ressourcen » Hier

Mathematische Distributionen und Verteilungen sind bei der Modellierung vieler Situationen im Unternehmen, besonders bei solchen, die mit Ungewissheit zusammenhängen, leistungsfähig und nützlich. Envision behandelt Distributionen und Verteilungen als Elemente erster Klasse und kann eine breite Auswahl an Berechnungen mit diesen ausführen. Auf all diese Operationen beziehen wir uns kollektiv als Algebra der Verteilungen, die von Envision unterstützt werden. In diesem Abschnitt stellen wir den distribution-Datentyp vor und bieten einen Überblick über die verschiedenen Operatoren und Funktionen, die darauf zutreffen.

Der Datentyp Distribution    Darstellung einer Verteilung    Punktweise Operationen    Verteilungen erstellen    Historische Entwicklungen

Der Datentyp Distribution

Mathematische Distributionen sind Objekte, die den Begriff der Funktion verallgemeinern. Unser Ziel in Envision ist etwas bescheidener und was wir Distributionen nennen, sind tatsächlich Funktionen $f: \mathbb{Z} \to \mathbb{R}$. Wir beziehen uns auf diese (mathematischen) Funktionen als Distributionen, da wir sie in Envision am häufigsten für Wahrscheinlichkeitsverteilungen verwenden, d.h. für positive Distributionen mit einer Masse gleich 1.

In Envision werden Verteilungen über einen bestimmten Datentyp, distribution genannt, umgesetzt. Andere Datentypen sind etwa number oder text. Der distribution-Datentyp bietet ein relativ komplexes Verhalten, gerade weil es mehr eine Funktion als ein Einzelwert ist. Zum Beispiel erstellen wir unten eine Delta-Distribution, also eine diskrete Funktion mit dem Wert 0 überall außer am Punkt 42, an dem der Wert bei 1 liegt.

d := dirac(42)

Verteilungen können auch als Datei mit dem Ion-Dateien exportiert werden. Doch Verteilungen können nicht als solche in CSV- oder Excel-Dateien exportiert werden.

Envision bietet viele andere Arten, Verteilungen zu erstellen, wie in den folgenden Abschnitten beschrieben wird.

Darstellung einer Verteilung

Verteilungen können mithilfe von Histogrammen visualisiert werden. Gehen wir von einer einfachen Poisson-Verteilung aus:



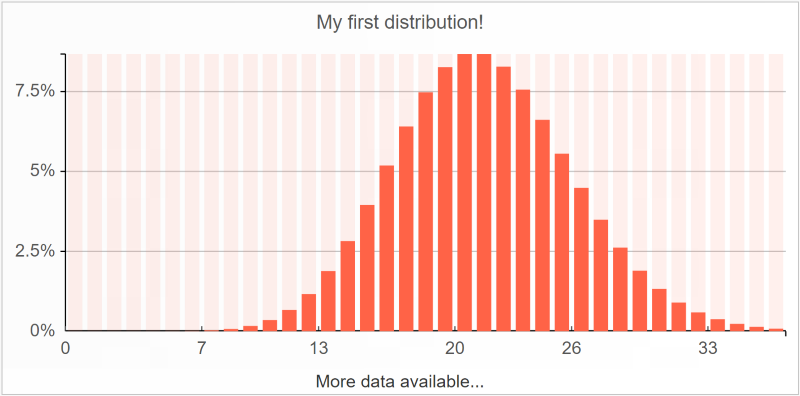
Dieser Darstellung wurde in Envision mit dem unten stehenden Einzeiler generiert:

show histogram "My first distribution!" tomato with
poisson(21)

Das histogram-Element erwartet eine einzige Skalarverteilung nach dem Schlüsselwort with.

Punktweise Operationen

Die einfachsten Operationen bei Verteilungen sind als punktweise Operationen bekannt. Wenn beispielsweise $f$ und $g$ zwei Verteilungen $\mathbb{Z} \to \mathbb{R}$ darstellen, können wir die Addition, wie folgt, definieren:

$$f+g: k \to f(k) + g(k)$$ Aus Envisions Sicht, wenn man davon ausgeht, dass sowohl X als auch Y Verteilungsvektoren sind, kann dieselbe Operation, auch wie folgt, geschrieben werden:

Z = X + Y

Dabei muss hervorgehoben werden, dass sogar, wenn es um Verteilungen geht, Envision weiterhin eine Vektorsprache bleibt. So wird gewöhnlich nicht nur eine einzige Verteilung zu einem Zeitpunkt verarbeitet, sondern ein ganzer Vektor von Verteilungen gleichzeitig. Dieselbe Operation kann auch aus einer Skalar-Perspektive so durchgeführt werden:

Z := X + Y

In diesem und in den nächsten Abschnitten, gehen wir, immer wenn wir X und Y in den Skript-Beispielen benutzen, davon aus, dass es sich bei diesen zwei Variablen um Verteilungen handelt.

Dann werden die punktweise Multiplikation und Subtraktion so definiert: $$f \times g: k \to f(k) \times g(k)$$ $$f-g: k \to f(k)-g(k)$$ was recht verständlich zur folgenden Syntax in Envision führt:

Z = X * Y
Z = Z - Y

Aus der Perspektive, dass eine Zahl $\alpha$ implizit zu einer konstanten Funktion $f_{\alpha}: k \to \alpha$ assimiliert werden kann, erlaubt Ihnen Envision, Zahlen und Verteilungen zu kombinieren - allerdings nur, wenn die Verteilung kompakt ist.

// OK, es ist kompakt
Z = 2 * X
// wird nicht durch Null geteilt ist OK
Z = X / 2
// falsch, keine kompakte Verteilung
Z = X + 1
// falsch, Y ist kompakt und hat Null-Werte
Z = X / Y

Die Verteilungen können auf verschoben werden. Der Verschiebungsoperator wird gewöhnlich, wie folgt, geschrieben:

$$f_{n}: k \to f(k+n)$$ Die entsprechende Envision-Syntax lautet:

Z = X << n // links Verschiebung
Z = X >> n // rechts Verschiebung

Natürlich funktioniert der Verschiebungsoperator weiter, wenn n negativ ist, doch dann wird aus einer links Verschiebung eine rechts Verschiebung und umgekehrt.

Verteilungen erstellen

Verteilungen können auf viele verschiedene Arten erstellt werden. Lokads Prognose-Engine erstellt Verteilungen für künftige Durchlaufzeiten oder den künftigen Bedarf. Wenn diese Verteilungen als Tabelle (*) serialisiert werden, ist es möglich, die Verteilung über die distrib()-Funktion zu erstellen. Die relevante Syntax hierfür lautet:

Demand = distrib(Id, G.Probability, G.Min, G.Max)

Die Variable Demand, die daraus entsteht, ist eine Verteilung. Wenn die Originaltabelle Segmente enthält, die länger als 1 sind, teilt distrib() gleichmäßig über das Segment aus. Die Masse der Verteilung wird durch die distrib()-Funktion gehalten.


Zusätzlich bietet Envision auch die Möglichkeit, eine Distribution direkt aus einem Set beobachteter Zahlenwerte zu erstellen. Dafür ist der ranvar()-Aggregator zuständig:

X = ranvar(Orders.Quantity)

Der ranvar()-Aggregator gibt eine Zufallsvariable zurück, die mit der beobachteten Häufigkeit der Aggregationsgruppen übereinstimmt. Wenn nichts zum Aggregieren vorliegt, gibt ranvar() dirac(0) zurück.

Zuletzt können Verteilungen aus einer Zeitreihe generiert werden, indem der ranvar.segment() Aggregator benutzt wird. D = ranvar.segment( // erstes Datum für jeden Artikel start: Items.Start // letztes Datum (einschließlich) für jeden Artikel end: Items.End // Länge des Zeitraums für jeden Artikel horizon: Items.Horizon // Integer zum Überspringen von Elementen step: Items.Step // das Datum jedes Ereignisses date: Orders.Date // die Anzahl jedes Ereignisses quantity: Orders.Quantity)

Es berechnet für jeden Artikel die Verteilung der Summe der Anzahl der Ereignisse für Zeiträume, deren Länge zwischen dem ersten und dem letzten Datum für diesen Artikel liegt. Gewöhnlich ist die Länge des Zeitraums die Durchlaufzeit eines Artikels.

===Verteilung in eine Tabelle erweitern===
In den vorangehenden Abschnitten haben wir gesehen, wie eine Tabelle in eine Verteilung aggregiert werden kann. Der umgekehrte Prozess, also die Erweiterung einer Verteilung auf Tabellenzeilen, ist auch möglich. In diesem Abschnitt analysieren wir die {{extend.distrib()}}-Funktion, die genau dafür gedacht ist. Die Syntax wird, wie folgt, veranschaulicht:

X = poisson(1) table G = extend.distrib(X) G.Probability = int(X, G.Min, G.Max) show table "My Grid" with Id G.Min G.Max G.Probability

Wobei {{X}} der Verteilungsvektor, der in Zeile 1 als Poisson-Verteilung erstellt wurde, ist. In Zeile 2 werden die Verteilungen in eine Tabelle namens {{G}} für Raster erweitert. Diese Tabelle hat eine Affinität {{(Id, *)}} und, wie in Zeilen 3 bis 7 dargestellt wird, wird die Tabelle mit den numerischen Spalten {{G.Min}} und {{G.Max}} ausgefüllt. Sowohl {{G.Min}} als auch {{G.Max}} sind ''inklusive Ränder''.

Wenn relativ kompakte Verteilungen erweitert werden, enthält die entstehende Tabelle gewöhnlich Zeile mit +1 Erhöhungen - also {{G.Min}} und {{G.Max}} um +1 von einer Zeile in die nächste erhöht. Doch gehen wir von Verteilungen mit hohen Werten aus, z.B. {{dirac(1000000)}}, wäre es äußerst ineffizient Millionen von Zeilen zu erstellen. Daher aggregiert die Funktion {{extend.distrib()}} große Verteilungen in dichtere Buckets. Dies erklärt, weshalb sowohl {{G.Min}} als auch {{G.Max}} vorliegen, die die ''inklusiven Ränder'' des Behälters darstellen.

Um mehr Kontrolle über die Granularität des erhaltenen Behälters zu erlangen, bietet die Funktion {{extend.distrib()}} die erste Überladung:

table G = extend.distrib(X, S)

wobei {{S}} ein Zahlenvektor ist. Die entstehende Tabelle bietet Behälter, die an die Segmente <nowiki>[0;0] [1;S]  [S+1; S+M] [S+M+1;S+2*M] ...</nowiki> ausgerichtet ist, wo {{M}} die standardmäßige Behältergröße ist, die auch ''Multiplikator'' genannt wird. Diese Überladung tritt gewöhnlicherweise dann ein, wenn der Bedarf über dem ''gesamten Bestand'' berücksichtigt werden muss.

Zuletzt bietet die zweite Überladung von {{extend.distrib()}} mehr Kontrolle mit:

table Grid = extend.distrib(X, S, M)

wobei {{M}} eine zwingende Behältergröße ist. Wenn {{M}} gleich null ist, fällt es auf die standardmäßige Behältergröße zurück, die von Envision automatisch angepasst wird. Diese zweite Überladung ist besonders nützlich, wenn ''Multiplikatoren für Losgrößen'' im Bestellprozess berücksichtigt werden müssen, da der Bedarf in Behälter einer bestimmten Größe aufgeteilt werden muss.

Achten Sie darauf, dass {{extend.distrib(X, S, M)}} je nach der Kapazität Ihres Lokad-Kontos fehlschlagen können, wen Sie versuchen, eine Verteilung mit hohem Wert zu erweitern, während Sie einen kleinen Multiplikator erzwingen.

===Faltung von Wahrscheinlichkeitsverteilungen===
[https://de.wikipedia.org/wiki/Faltung_(Mathematik)|Faltungen] stellen eine fortgeschrittenere Art von Operationen mit Verteilungen dar. Die Hauptanwendung von Faltungen hängen mit ''Zufallsvariablen'' zusammen. Im Gegensatz zu den punktweisen Operationen, bieten Faltungen probabilistische Interpretationen, wie die Summe oder Multiplikation von Zufallsvariablen. Faltungen können in Envision an ihren zwei Operatoren, die mit {{*}} enden, erkannt werden. nämlich:

// additive Faltung Z = X +* Y // subtraktive Faltung, gleich wie X +* reflect(Y) Z = X -* Y // multiplikative Faltung Z = X ** Y // Faltungspotenz Z = X ^* Y @@ Die additive (bzw. substraktive) Faltung kann als Summe (bzw. Differenz)zweier unabhängiger Zufallsvariablen $X+Y$ (bzw. $X-Y$) gedeutet werden. Die multiplikative Faltung, auch als Dirichlet-Faltung bezeichnet, kann als das Produkt zweier unabhängiger Zufallsvariablen interpretiert werden.

Die Faltungspotenz ist etwas komplexer und stellt Folgendes dar: $$X ^ Y = \sum_{k=0}^{\infty} X^k \mathbf{P}[Y=k] \text{ wo } X^k = X + \dots + X \text{ ($k$ Mal)}$$ Diese letzte Operation ist aufgrund ihres Bezugs zum Prozess der integrierten Bedarfsprognose interessant, bei der $X$ den täglichen Bedarf, der als stationär betrachtet wird, und $Y$ die probabilistischen Durchlaufzeiten darstellt.

Siehe auch unsere Seite zu Faltungspotenz.

Historische Entwicklungen

Lokads Prognose-Engine begann Anfang 2015 Quantiltabellen zu bieten. Diese Tabellen waren noch nicht genau, Wahrscheinlichkeitsverteilungen - nur interpolierte Quantilprognosen - doch wir waren schon ziemlich nahe. Bei der Arbeit mit unseren Kunden bemerkten wir das riesige Potential der Anwendung von probabilistischen Analysen auf quantitative Lieferkettenoptimierung. Doch unsere Tabellen war nur das: lange Tabellen, in denen alle Wahrscheinlichkeiten aufgelistet waren. Während diese Tabellen für unsere Kunden und auch für uns einen Durchbruch darstellten, merkten wir bald, dass die Verarbeitung der Wahrscheinlichkeiten in Form von Listen keine leichte Aufgabe war.

Die Algebra der Verteilungen ist Lokads breite technische Antwort auf die Herausforderungen der Lieferkette im Zusammenhang mit ungewissen Zukunftsszenarien. In solchen Fällen reicht es nicht mit einer einfachen Mittelwertprognose. Hier ist eine komplexe Risikoanalyse aller Möglichkeiten erforderlich. Envision begrüßt die Idee, dass alle Szenarien in Betracht gezogen werden sollten, statt sich nur auf eine Handvoll von ihnen zu konzentrieren. Zu diesem Zweck können über Envision-Skripte Zufallsvariablen eingeführt und durch spezifische Funktion für Zufallsvariablen, wie etwa Faltungen, bearbeitet werden. Genaueres folgt. In der Praxis stellt die Algebra der Verteilungen eine elegante Lösung zur Modellierung komplexer Fälle bei Lieferketten dar, bei denen sowohl der künftige Bedarf, als auch die künftigen Durchlaufzeiten ungewiss sind.