LokadTV
Блог
контакт
Вход
Ru
Español English Français Deutsch Italiano Русский 中文

Квантильная регрессия

Жоаннес Верморель, февраль 2012 г.

Квантильная регрессия — это регрессия (т.е. прогноз), которая намеренно вводит смещение в результат. Вместо поиска среднего значения прогнозируемой переменной, квантильная регрессия направлена на поиск медианы и любых других квантилей (которые иногда называют процентилями). Квантили особенно полезны для оптимизации товарных запасов в качестве прямого метода для вычисления точки возобновления.

Здесь регрессия выступает синонимом прогноза. "Регрессия" делает акцент на математическом подходе, тогда как "прогноз" - на практическом использовании результата.

Понятие квантильной регрессии представляет собой относительно продвинутую область статистики, поэтому цель данной статьи заключается не в строгом толковании этого предмета, а в интуитивно-понятном введении в него для практических специалистов, работающих в сфере розничной торговли или промышленного производства.

Наглядное представление квантилей

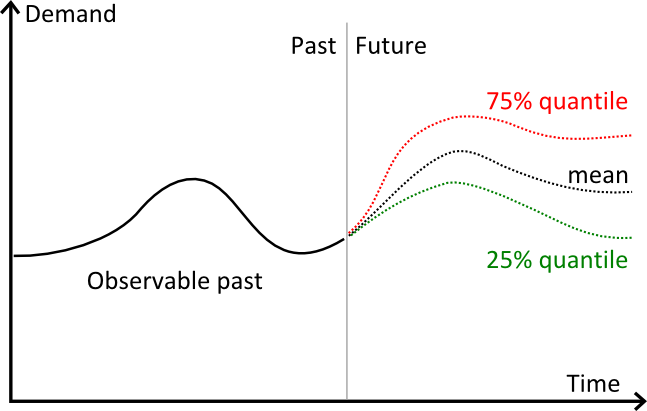
The lower and upper quantile time-series side-by-side with the mean forecast time-series.

На графике показаны 3 обособленных прогноза:
  • красным цветом отмечен 75-процентный квантильный прогноз.
  • черным цветом отмечен прогноз на основе средних значений.
  • зеленым цветом отмечен 25-процентный квантильный прогноз.

Визуально поведение квантилей схоже с поведением доверительных интервалов. Однако, на практике квантиль нужен лишь для процентного выражения отдельно взятых точек.

Квантили (процентили) будущего спроса

Классическим и наиболее понятным прогнозом является прогноз на основе средних значений: соответствующие веса перепрогнозирования и недопрогнозирования должны быть равными, в противном случае прогноз становится смещенным (точнее смещенным относительно среднего значения).

И хотя несмещенный прогноз является желаемым результатом, он не имеет ничего общего с точностью прогноза. В частности, прогноз может быть одновременно несмещенным и крайне неточным. Смещение связано лишь с тенденцией модели прогнозирования переоценивать или недооценивать будущее.

Первой доработкой этого подхода является медианный прогноз: соответствующая частота перепрогнозирования и недопрогнозирования должна быть равной, в противном случае прогноз становится смещенным относительно медианы.

На данном этапе мы перенесли понятие несмещенных прогнозов с равных весов на равную вероятность. Этот перенос не очевиден, но в некоторых ситуациях он может иметь огромное числовое значение.

Практический пример: Средний и медианный семейный доход в США

Семейный доход демонстрирует существенные различия между средним и медианным значениями.

По данным Бюро переписи населения США, в 2004 г. медианный семейный доход составлял 44 389 долларов США, тогда как средний доход составлял 60 528 долларов США, превышая медианный доход на 40%.

Это несоответствие объясняется противопоставлением (сравнительно) высоких доходов наиболее богатых семей и доходов прочего населения. Несоответствие между средним и медианным значениями обнаруживается во всех несимметричных распределениях, как правило, во всех распределениях, отличных от нормального.

Генерализация медианного значения

Медианное значение представляет собой пороговое значение, в котором распределение разбивается с вероятностью 50/50. Однако, возможно рассмотрение и других частотных коэффициентов. Например, мы можем рассматривать коэффициенты 80/20, 90/10 и любые другие, если их общее значение составляет 100%.

Квантили представляют собой генерализацию медианного значения до любого процентного выражения. Для τ, значение которого находится между 0 и 1, квантильная регрессия Q(τ) представляет собой пороговое значение, при котором вероятность появления значения, ниже порогового, равна τ.

Квантильные прогнозы

Как классические, так и квантильные прогнозы, используют временные ряды в качестве вводимых параметров. Временные ряды являются вводимыми данными. Помимо этих данных, для классического прогноза временных рядов на основе средних значений нужны два дополнительных параметра:

  • период (день, неделя или месяц).
  • горизонт - целое число, обозначающее количество прогнозируемых периодов.

Обобщение временных рядов производится по периодам, а величина горизонта выбирается таким образом, чтобы прогноз имел практическую пользу, как правило, это значение превышает время выполнения заказа.

Прогнозы на основе средних значений получают преимущество благодаря своему удобному свойству: сложение прогнозов является правильным с точки зрения математики. Например, если y1, y2, y3 и y4 - это прогнозы на 4 последующих недели, мы можем получить ожидаемый спрос на две последующих недели, сложив y1+y2.

Однако, сложение квантильных прогнозов с математической точки зрения является неправильным, а точнее сумма квантилей не равна квантилю суммы (суммы сегментов).

Рассмотрим пример, объясняющий невозможность сложения квантилей. Предположим, что некто еженедельно опускает 1 доллар США в игровой автомат. Предположим, что вероятность выиграть 50 долларов США составляет 1%. Если мы посмотрим на 99-процентный квантиль ожидаемого выигрыша, еженедельный выигрыш будет составлять 50 долларов США. Однако, если мы посмотрим на 99-процентный квантиль, покрывающий две недели, ожидаемый выигрыш по-прежнему будет составлять 50 долларов США. Действительно, вероятность двух выигрышей составляет лишь 0,01% (1% умножить на 1%), а значит 99-процентный квантиль остается неизменным. Сложение двух 99-процентных квантилей будет равно 100 долларам США, но в реальности накопление этой суммы при 99-процентных квантилях займет 16 недель (мы не приводим доказательство этого численного результата, так как оно выходит за рамки этой статьи).

Так как сложение квантильных прогнозов невозможно, для квантильных прогнозов временных рядов необходимо переосмысление периода обобщения. Действительно, создание квантильных прогнозов на периоды является спорным, поскольку объединение таких элементарных прогнозов для создания правильных квантилей, покрывающих целые сегменты, невозможно.

Таким образом, квантильный прогноз временных рядов имеет определенную структуру:

  • τ - целевой квантиль в процентном выражении.
  • λ - выражающий продолжительность горизонт (обычно в днях).

Например, если временные ряды отражают продажи продукта А, а параметры имеют следующие значения: τ=0,90 и λ=14 дней, квантильный прогноз (τ, λ) будет давать значение спроса, имеющее 90-роцентную вероятность оказаться выше суммарного объема спроса, наблюдаемого на протяжении 14 дней (и соответственно 10-процентную вероятность оказаться ниже суммарного объема спроса, наблюдаемого на протяжении тех же 14 дней).

В отличие от классических прогнозов, квантильные прогнозы рассчитывают одно значение на один временной ряд независимо от горизонта. До определенного масштаба квантильные прогнозы являются более агностическими по отношению к периодам, чем их классические аналоги.

Фишка Lokad

На первый взгляд квантильные прогнозы кажутся более сложными, чем классические. Так или иначе, во многих реальных ситуациях практические специалисты прекращают использовать прогнозы на основе средних значений и мгновенно экстраполируют их в виде квантильных прогнозов, как правило, допуская при этом, что прогнозы имеют нормальное распределение. Однако, такая экстраполяция чаще всего является наиболее слабым звеном процесса прогнозирования и может значительно ухудшить окончательный результат. Технология прогнозирования должна адаптироваться в соответствии с практическими требованиями, то есть предоставлять оригинальные квантильные прогнозы, а не наоборот.

Дополнительные материалы