Расчет объема резервных запасов через прогнозирование продаж и Excel

Жоаннес Верморель, декабрь 2007 г. (Последняя редакция — январь 2012 г.)


Это руководство объясняет, как оптимизировать товарные запасы, приведя уровень резервных запасов к оптимальной величине. Это руководство относится к розничной торговле и производству. Теория представлена с помощью Microsoft Excel. Более подробные материалы доступны для разработчиков программного обеспечения, желающих воспроизвести теорию в адаптированном приложении.

Введение    Модель пополнения запасов       Нормальное распределение ошибки       Уравнение товарного запаса       Соответствие времени заказа и периода прогнозирования    Использование Excel для вычисления точки заказа    Примечания для разработчиков    Ресурсы

Целевая аудитория: Этот документ нацелен в основном на профессионалов сети поставок в розничной торговле или производстве. Тем не менее, этот документ также полезен для специалистов по программному обеспечению в бухгалтерском учете, системах управления ресурсами, электронной коммерции, которые хотят расширить возможности своих приложений с помощью элементов управления товарными запасами.

Мы постарались свести математические требования к минимуму. Тем не менее, мы не можем совсем исключить формулы, так как основное назначение данного документа - служить практическим руководством, которое объясняет, как рассчитать резервный товарный запас.

Загрузить: calculate-safety-stocks.xls (таблица Microsoft Excel)

Введение

Управление товарными запасами — это финансовое компромиссное решение между издержками на хранение товара и издержками в связи с отсутствием товара. Чем больше товарные запасы, тем больше необходимо оборотных средств и тем больше обесцениваются товарные запасы. С другой стороны, при недостатке товара, вы можете столкнуться с ситуацией дефицита, упустить потенциальные продажи, и, возможно, даже нарушить весь процесс производства.

Товарные запасы, в основном, зависят от двух факторов

• спрос в ходе выполнения заказа: количество товара, которое будет потреблено или куплено.
• время заказа: время отсрочки между заказом товара и его поступлением в продажу.
  

Эти два фактора несут в себе неопределенность

• изменения спроса: поведение потребителей может меняться довольно не предсказуемо.
• изменения времени заказа: поставщики или транспортные агенты могут столкнуться с непредвиденными трудностями.
  

Решение относительно объема резервного товарного запаса косвенно равноценно решению о компромиссе между издержками, принимая во внимание эти неопределенности.

Баланс между издержками на содержание товарного запаса и издержками в связи с дефицитом товаров очень зависит от типа бизнеса. Следовательно, вместо рассмотрения этих издержек напрямую, мы введем классическое понятие вероятности обслуживания.

Уровень обслуживания отражает вероятность, что определенный уровень товарных запасов не приведет к нехватке товара. Естественно, что при увеличении товарных запасов, увеличивается и уровень обслуживания. Когда товарные запасы становятся очень большими, уровень обслуживания стремится к величине 100% (то есть вероятность возникновения дефицита товаров равна нулю).

Выбор вероятности обслуживания, то есть приемлемой вероятности возникновения дефицита, находится вне области рассмотрения данного руководства, однако вы можете прочитать отдельную статью о расчете оптимальной вероятности обслуживания.

Модель пополнения запасов

Точка заказа - это уровень товара, который должен сигнализировать о необходимости заказа. Если бы не было неопределенности (т.е. известен будущий спрос и предложение надежно), точка заказа равнялась бы прогнозируемому спросу во время периода отсрочки заказа, также называемому спрос во время отсрочки заказа.

В реальности, из-за неопределенности, мы имеем
точка заказа = спрос на время отсрочки заказа + резервный запас

Если условиться, что прогноз объективен (со статистической точки зрения), наличие нулевого уровня товарных запасов приведет к уровню обслуживания 50%. Объективность прогноза означает, что одинаков шанс того, что будущий спрос окажется больше или меньше спроса во время отсрочки заказа (следует помнить, что спрос во время отсрочки заказа - это лишь прогнозируемая величина).

Внимание: прогнозы могут быть объективными, не будучи точными. Необъективность указывает на систематическую ошибку в модели прогнозирования (например: всегда переоценивать спрос на 20%).

Нормальное распределение ошибки

В этот раз, нам нужен способ представить неопределенность спроса во время отсрочки заказа. В дальнейшем, мы предположим, что эта ошибка имеет нормальное распределение, см. рисунок ниже.



Статистические заметки: предположение о нормальном распределении не является полностью произвольным. При определенных условиях, статистические приближения приходят к нормальному распределению, как описано в Теореме центрального лимита. Но эти предположения не входят в область рассмотрения данного руководства.

Нормальное распределение определяется всего двумя параметрами: его математическим ожиданием и отклонением. Так как мы сделали предположение об объективности прогнозов, мы принимаем математическое ожидание и распределение ошибки равными нулю, что не означает, что мы принимаем значение ошибки за ноль.

Определение отклонения ошибки прогноза является более сложным задачей. Lokad, как и большинство инструментов прогнозирования, выдает значение САОП (средняя абсолютная ошибка в процентах) вместе с прогнозами. Для полноты описания, мы объясним, как можно преодолеть эту проблему, используя простую эвристику.

В частности, отклонение в пределах данных прошлых периодов можно использовать в качестве объекта исследований для определения примерного отклонения прогноза. Дэвид Пьясеки (David Piasecki) предлагает использовать прогнозируемый спрос вместо среднего значения спроса в формуле отклонения, то есть
σ2 = E[ (yt - y')2 ]
где E - оператор среднего значения, yt - значение спроса в прошлом периоде t (обычно объем продаж) и y' - прогнозируемый спрос.

Ключевая идея этого предположения - это то, что ошибка прогноза очень часто связана с величиной ожидаемого отклонения: чем больше будущее отклонение, чем больше ошибка прогноза .

В действительности, при вычислении для этой ошибки используется несколько хитростей, которые будут подробно рассмотрены ниже.

Уравнение товарного запаса

На данном этапе бы дали определение математическому ожиданию и отклонению, таким образом, распределение ошибки известно. Сейчас нам необходимо вычислить допустимое значение ошибки в рамках этого распределения. Для этого мы ввели понятие уровня обслуживания ( в процентах).

Примечание: Мы предполагаем, что время заказа статично. Тем не менее, очень похожий подход можно использовать для переменного времени заказа. Смотреть:

• Понятие переменного времени заказа
• Моделирование переменного времени заказа
  

Для того чтобы перевести уровень обслуживания в уровень ошибки, также называемый фактором обслуживания, мы должны использовать обратное совокупное нормальное распределение (иногда называемое обратным нормальным распределением) (см. NORMSINV (обратное нормальное распределение), чтобы найти соответствующую функцию в Excel) Это может выглядеть сложным, но, на самом деле, это не так. Предлагаем вам ознакомиться с сетевым приложением нормального распределения для получения лучшего визуального представления. Как вы можете видеть, общая формула преобразует проценты в область-под-изгибом, при этом на оси отражается величина уровня обслуживания.

Интуитивно, мы вычисляем
резервный товарный запас = стандартное отклонение ошибки * фактор обслуживания

Более формально, предположим, что S - это резервный товарный запас, тогда
S = σ * cdf(P)
где σ - это стандартное отклонение (т.е. квадратный корень из σ2 при условии фиксированного отклонения), cdf нормализованное общее нормальное распределение(математическое ожидание равно нулю и отклонение равно единице) и P - это уровень обслуживания.

Помня что
точка заказа = спрос во время выполнения заказа + резервный товарный запас
Предположим, что R - это точка заказа, тогда имеем
R = y' + σ * cdf(P)

Соответствие времени заказа и периода прогнозирования

До этого времени, мы просто предполагали, что для данного времени заказа, мы можем получить соответствующий прогноз будущего спроса. На практике это работает не совсем так. Анализ данных прошлых периодов обычно начинается с объединения данных во временные периоды (обычно недели или месяцы).

Так, выбранный период не обязательно совпадает со временем заказа. Таким образом, для выражения спроса в период отсрочки получения заказа и соответствующих его отклонений требуются некоторые дополнительные вычисления (принимая нормальное распределение ошибок в прогнозе, как было оговорено выше).

Интуитивно, спрос во время отсрочки получения заказа можно вычислить как сумму прогнозируемых величин для будущих периодов которые пересекают сегмент времени заказа. Нужно быть осторожными для правильной адаптации последнего прогнозируемого периода.

Формально, пусть T - это период и L - это время заказа. Мы имеем
L = k * T + α * T
где k - это целое число и 0 ≤ α < 1. Пусть D - это спрос в период отсрочки получения заказа. Тогда, получаем окончательное уравнение для спроса во время отсрочки получения заказа
D = (Σt=1..k y't) + αy'k+1
где y'n - это прогнозируемый спрос для nго периода в будущем.

Принимая такие предположения по поводу нормального распределения, мы можем вычислить отклонение ошибки прогноза как
σ2 = E[ (yt - y')2 ]
где y' - это средний прогноз на период
y'= D / (k + α)

Но σ2 здесь рассчитывается как переменная в периоде в то время как нам нужна переменная, которая бы совпадала с временем отсрочки заказа. Пусть σL2 будет адаптирована как переменная во времени отсрочки заказа, тогда имеем
σL2 = (k + α) σ2

Наконец, мы можем переписать уравнение для точки заказа как
R = D + σL * cdf(P)

Использование Excel для вычисления точки заказа

В этой части рассказывается, как вычислить точку заказа, используя Microsoft Excel. Мы рекомендуем ознакомиться с примером таблицы Excel.



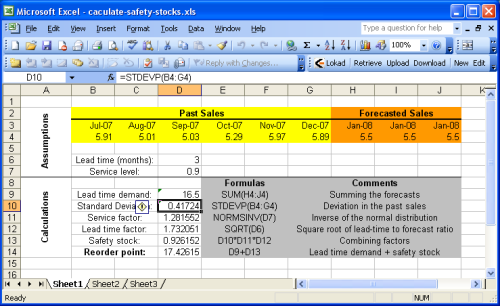
Таблица в примере разделена на две секции: предположения наверху и вычисления внизу. Предполагается, что прогнозы являются частью предположений, так как прогнозирование продаж (спроса) не входит в область рассмотрения данного руководства. Детали изложены в нашем Руководстве по прогнозам в Excel.

Большинство формул, представленных в предыдущей части, являются очень простыми операциями (сложение, умножение), которые легко произвести в Excel. Тем не менее, необходимо обратить внимание на две функции:

• NORMSINV (Microsoft KB): вычисляет приблизительное значение общего нормального распределения, обозначенного нами как cdf.
• STDEV (Microsoft KB): вычисляет примерное значение стандартного отклонения, обозначенного σ. Мы помним, что стандартное отклонение σ - это квадратный корень отклонения σ2.
  

Для упрощения первый лист не предполагает вычислений по правилу 80% σ2 = E[ (yt - y')2 ] при расчете фактора обслуживания. Этот подход используется на Sheet2 (втором листе таблицы Excel). Так как для примера мы взяли стационарные прогнозы, точка заказа остается идентичной с использованием эвристического правила или без него.

Примечания для разработчиков

Это раздел предназначен для разработчиков, которые хотят применить модель пополнения запасов в автоматической системе управления товарными запасами.

Большинство формул в этом руководстве могут быть легко применены с помощью обычных инструментов разработки. Если вы работаете с .NET, мы рекомендуем использовать Math.NET Iridium, математическую библиотеку с открытым исходным кодом, написанную на C#, в которой есть и стандартное отклонение, и функция общего нормального распределения.

В другом случае стандартное отклонение можно легко внедрить, основываясь на его определении, см. страница Wikipedia. Общее нормальное отклонение немного сложнее, но Питер Аклам (Peter J. Acklam) предлагает хороший алгоритм который был использован на многих языках. Код для этих двух методов должен быть не более 20-30 строк.

Ресурсы

Управление запасами и планирование производства, Эдвард А. Силвер, Дэвид Ф. Пайк, Рейн Петерсон, Уайли; 3-е издание, 1998 г.