Жоаннес Верморель, февраль 2012 годаФункция потерь пинбольного шарика — это метрика, которая используетс для оценки точности квантильного прогноза.
Оценка
точности квантильного прогноза представляет собой хитроумную задачу. В отличие от классических прогнозов, целью которых является создание прогноза, наиболее близкого к наблюдаемым величинам, в случае же с квантильными прогнозами ситуация
смещается (с определенной целью). Таким образом, наивное сравнение
наблюдаемых и
прогнозируемых величин является неудовлетворительным.
Функция потерь пинбольного шарика возвращает значение, которое может быть интерпретировано как
точность модели квантильного прогнозирования.
Формула
Пусть $\tau$ - желаемый квантиль, $y$ - реальное значение и $z$ - квантильный прогноз, тогда $L_\tau$ (функция потерь пинбольного шарика) может быть записана как:
$$
\begin{eqnarray}
L_{\tau}(y,z) & = & (y - z) \tau & \textrm{ if } y \geq z \\\
& = & (z - y) (1 - \tau) & \textrm{ if } z > y
\end{eqnarray}
$$
Скачать: pinball-loss-function.xlsxФайл демонстрирует, как вычислить функцию потерь пинбольного шарика в Microsoft Excel. Фактическая формула не сложнее большинства показателей точности таких, как средняя абсолютная ошибка в процентах.
Рисунок
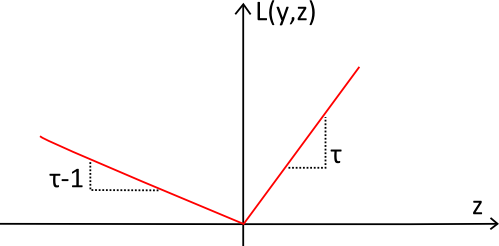
Функция потерь пинбольного шарика (показана красным) была названа за свою форму, напоминающую траекторию шарика в
пинболе. Эта функция всегда положительна, и чем дальше от желаемого значения $y$, тем больше значение $L_\tau(y,z)$.
Наклон линии используется для того, чтобы отразить
желаемый дисбаланс в квантильном прогнозе.
Лучшая квантильная модель имеет наименьшие потери пинбольного шарика
Наиболее важный результат, связанный с функцией потерь пинбольного шарика заключается в том, что
чем меньше потери пинбольного шарика, тем точнее квантильный прогноз.
Можно доказать, что функция минимизирующая потери пинбольного шарика также обеспечивает оптимальный квантиль. Однако необходимый для доказательства формализм выходит за рамки этой статьи.
Таким образом, чтобы сравнить точность двух квантильных моделей (Lokad против модели конкурентов), достаточно вычислить
средние потери пинбольного шарика для каждой модели в сериях испытаний. Их количество должно быть достаточно большим, чтобы убедиться в статистической значимости наблюдаемых различий. На практике нескольких сотен таких серий достаточно, чтобы оценить, какая квантильная модель является самой
точной.
Фишка Lokad
На наш взгляд, предполагаемая
простота понятия точности для классических прогнозов (т.е. прогнозов на основе средних значений) по сильно преувеличена. Как прогнозы на основе средних значений, так и квантильные прогнозы, подвержены
переобучению, которое значительно усложняет сравнение моделей прогнозирования. Однако функция потерь пинбольного шарика является крайне простым способом оценки
относительной точности двух моделей квантильного прогнозирования.
Дополнительные материалы
