Por Joannès Vermorel, febrero de 2012La función de pérdida
pinball, también llamada pérdida cuantílica, es una métrica utilizada para evaluar la precisión de un pronóstico cuantílico.
Evaluar la
precisión de un
pronóstico cuantílico es un problema sutil. De hecho, al contrario de los pronósticos clásicos, en los que el objetivo es obtener un pronóstico lo más cercano posible a los valores observados, la situación es
desviada (adrede) cuando se trata de los pronósticos cuantílicos. Así, la comparación inocente y rígida entre situación
observada y
pronósticos no es satisfactoria. La
función de pérdida pinball es una función simple que reporta la
precisión de dos modelos de pronóstico cuantílicos.
Fórmula
Tomemos como cuantil objetivo $\tau$ , $y$ como el valor real y $z$ como el pronóstico cuantílico; luego, la PLF (función de pérdida
pinball) se desarrollaría del siguiente modo:
$$
\begin{eqnarray}
L_{\tau}(y,z) & = & (y - z) \tau & \textrm{ if } y \geq z \\\
& = & (z - y) (1 - \tau) & \textrm{ if } z > y
\end{eqnarray}
$$
Descargar: pinball-loss-function.xlsxLa hoja de cálculo ilustra el modo de calcular la función de pérdida
pinball en Microsoft Excel. La fórmula real no es más complicada que la mayoría de los indicadores de precisión, como el MAPE.
Ilustración
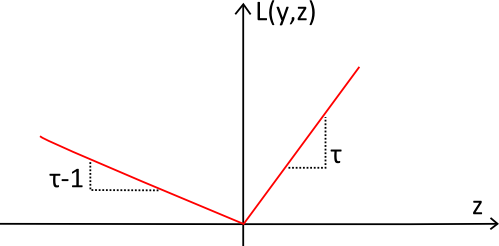
La función de pérdida
pinball (en rojo) lleva ese nombre por su forma, muy similar a la trayectoria de la bola en un
pinball. La función es siempre positiva y, cuanto más se aleja del objetivo $y$, mayor es el valor de $L(y,z)$. La
pendiente se utiliza para reflejar el
desequilibrio deseado en el pronóstico cuantílico.
El mejor modelo cuantílico tiene la menor pérdida pinball
El resultado más importante asociado con la función de pérdida
pinball es que
cuanto menor es la pérdida pinball, más preciso es el pronóstico cuantílico.
Puede probarse que la función que minimiza la pérdida pinball da también el cuantil óptimo. Sin embargo, el formalismo necesario para la prueba excede el objetivo de este artículo.
Por lo tanto, para comparar la precisión de dos modelos cuantílicos (por ejemplo, Lokad vs. otro), es suficiente calcular la pérdida pinball
promedio de cada modelo en una cantidad de series lo suficientemente grande como para asegurarse de que la diferencia observada sea estadísticamente significativa. En la práctica, unos cientos de series de tiempo serán suficientes para evaluar qué modelo cuantílico es el más
preciso.
La solución de Lokad
En nuestra opinión, la supuesta
simplicidad de la noción de precisión para un pronóstico clásico (es decir, un pronóstico medio) está sobrestimada. Los pronósticos, tanto de media como cuantílicos, están sujetos a un sobreajuste, que complica bastante la comparación de los modelos de pronóstico. Sin embargo, la función de pérdida
pinball constituye un modo simple de evaluar la precisión
relativa de dos modelos de pronóstico cuantílicos.
Lectura adicional
- Sequential Quantile Prediction of Time Series (Predicción cuantílica secuencial de series de tiempo), de Gerard Biau y Benoit Patra, Teoría de la Información, IEEE Transactions, marzo de 2011
- Puntuaciones de rango de probabilidad continuo (CRPS), una generalización de la función de pérdida pinball para los pronósticos probabilísticos
