Por Joannès Vermorel, febrero de 2012La regresión cuantílica es un tipo de regresión (es decir, pronóstico) que introduce
adrede una desviación en el resultado. En lugar de buscar la
media de la variable que será pronosticada, una regresión cuantílica busca la
mediana y cualquier otro cuantil (a veces llamados
percentiles). Los cuantiles son particularmente
útiles para la optimización del inventario como método directo para calcular el
punto de reorden.
Aquí, regresión se utiliza como sinónimo de pronóstico. "Regresión" enfatiza el método matemático, mientras que "pronóstico" enfatiza el uso práctico que se hace del resultado.
La noción de regresión cuantílica es un tema estadístico relativamente avanzado, y el objetivo de este artículo no es tratar el tema en profundidad, sino solo dar una introducción (relativamente) intuitiva al tema para quienes trabajan en el comercio minorista o la fabricación.
Ilustración visual de cuantiles
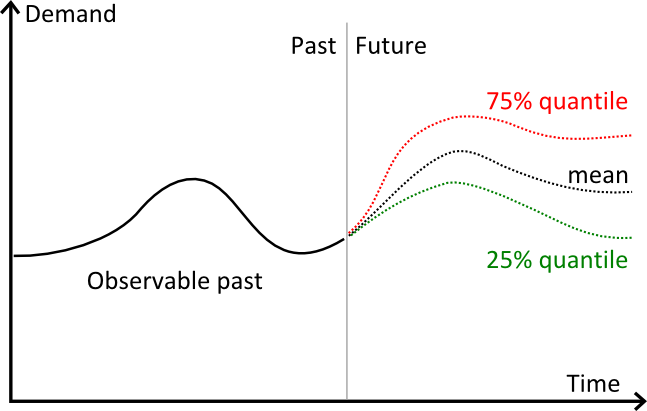
El gráfico anterior ilustra 3 pronósticos distintos:
- en rojo, pronósticos cuantil 75 %.
- en negro, un pronóstico de media.
- en verde, pronósticos cuantil 25%.
Visualmente, los cuantiles se comportan en modo similar a los intervalos de confianza. Sin embargo, en la práctica, el cuantil solo se necesita para un solo porcentaje objetivo.
Cuantiles (o percentiles) de la demanda futura
El pronóstico clásico y más intuitivo es el
pronóstico de media: los
pesos de sobrepronosticar y subpronosticar deberían ser iguales; de lo contrario, el pronóstico es
sesgado (más precisamente,
sesgado con respecto a la media).
Si bien contar con un pronóstico sin desviaciones es algo deseable, no dice nada sobre la precisión del pronóstico. En particular, un pronóstico puede al mismo tiempo no presentar desviaciones y ser ampliamente inexacto. La desviación solo hace referencia a la propensión del modelo de pronóstico a sobrestimar o subestimar el futuro.
Un primer refinamiento de esta visión es el
pronóstico de mediana: la
frecuencia de sobrepronosticar o subpronosticar debería ser igual; de lo contrario, los pronósticos serían
sesgados con respecto a la mediana.
A este punto, ya hemos pasado la noción de pronósticos
sin desviaciones de
pesos iguales a
probabilidades iguales. Este cambio es sutil, pero en algunas situaciones podría tener un importante impacto numérico.
Ilustración: Ingreso familiar medio vs. ingreso familiar mediano en Estados Unidos
El
ingreso familiar ilustra la profunda diferencia entre media y mediana.
Según el US Census Bureau, en el 2004, el ingreso familiar mediano era de $44.389, mientras que el mismo año, el ingreso medio era de $60.528, casi un 40 % mayor que el mediano.
La explicación de esta discrepancia se encuentra en el alto nivel (comparativamente) de los ingresos estadounidenses más ricos comparados con los del resto de la población. Esa discrepancia entre media y mediana se encontrará en todas las distribuciones que no sean simétricas, generalmente en todas las distribuciones que no siguen una distribución normal.
Generalización de la mediana
La mediana representa el umbral en el que la distribución se divide en 50/50. No obstante, es posible considerar
otras razones de frecuencia. Por ejemplo, podemos considerar 80/20 o 90/10 o cualquier otra razón en la que el total sigue siendo el 100 %.
Los cuantiles representan una
generalización de la mediana a cualquier porcentaje. Para τ, un valor entre 0 y 1, la regresión cuantílica Q(τ) representa el umbral en el que la probabilidad de observar un valor menor que el umbral es exactamente τ.
Pronósticos cuantílicos
Tanto los pronósticos clásicos como los cuantílicos toman una
serie de tiempo como dato de entrada. La serie de tiempo representa el dato de entrada. Además de los datos, un pronósticos clásico de serie de tiempo
de media requiere dos parámetros estructurales adicionales:
- el período, como día, semana o mes.
- el horizonte, un número entero que representa la cantidad de períodos a ser pronosticados.
Implícitamente, la serie de tiempo es agregada según el
período, y el horizonte se elige lo suficientemente amplio como para ser de uso práctico, generalmente mayor que el
tiempo de entrega.
Los pronósticos
de media se benefician de una propiedad muy útil: es
matemáticamente correcto sumar los pronósticos. Por ejemplo: si
y1,
y2,
y3 e
y4 representan las 4 semanas de pronóstico por adelantado, entonces si necesitamos la demanda esperada
solo para las siguientes
dos semanas, podemos sumar
y1+y2.
Sin embargo,
sumar los pronósticos cuantílicos es matemáticamente incorrecto o, más precisamente, la suma de los cuantiles no da el cuantil de la suma (suma de los segmentos).
Ilustremos la razón por la que el cuantil no puede ser sumado. Supongamos que tenemos un jugador que juega una moneda de US$ 1 en una máquina tragaperras cada semana. Supongamos que las posibilidades de ganar sean del 1 % por un premio de US$ 50; de lo contrario, el premio es igual a 0. Si observamos el cuantil 99 % de la recompensa esperada, tenemos una recompensa de US$ 50 cada semana. Sin embargo, si observamos el cuantil 99 % de dos semanas, la recompensa esperada sigue siendo igual a US$ 50. De hecho, la probabilidad de ganar dos veces es solo del 0,01% (1 % multiplicado por 1 %); así, el cuantil 99 % se mantiene sin cambios. La suma de los dos cuantiles 99 % semanales daría US$ 100, pero en realidad llevaría 16 semanas acumular US$ 100 de ganancia para el cuantil 99 % (la prueba de este resultado numérico no está dada, ya que excedería el objetivo de este artículo).
Debido a que los pronósticos cuantílicos no pueden sumarse, los pronósticos cuantílicos de series de tiempo deben
reconsiderar la noción misma de agregación de período. De hecho, elaborar pronósticos cuantílicos
por período es discutible, porque esos pronósticos
elementales no pueden combinarse para elaborar cuantiles correctos sobre los segmentos.
Así, el pronóstico
cuantílico de series de tiempo viene con una estructura distintiva:
- τ el cuantil objetivo, un porcentaje.
- λ el horizonte expresado como una duración (generalmente en días).
Por ejemplo, si la serie de tiempo representa las ventas de un producto A y tenemos los parámetros τ=0.90 y λ=14 días; luego, el pronóstico cuantílico (τ, λ) dará el valor de la demanda que tiene exactamente el 90 % de probabilidad de ser mayor que la demanda total observada en 14 días (respectivamente, 10 % de probabilidad de ser menor que la demanda en los mismos 14 días).
Al contrario de los pronósticos clásicos, los pronósticos cuantílicos elaboran
uno y solo un valor por serie de tiempo, independientemente del horizonte. En cierta medida, los pronósticos cuantílicos desconfían más el período que los pronósticos clásicos.
La solución de Lokad
A primera vista, los pronósticos cuantílicos parecen algo más complicados que los clásicos. Sin embargo, en muchas situaciones de la vida real, los encargados acaban por elaborar, primero, pronósticos de
media para luego
extrapolarlos inmediatamente como pronósticos cuantílicos, suponiendo generalmente que los pronósticos siguen una distribución normal. Sin embargo, este paso de extrapolación representa a menudo el enlace más débil del proceso, y puede degradar significativamente el resultado final. La tecnología de pronóstico debería adaptarse a las necesidades prácticas, es decir, dar pronósticos cuantílicos nativos, y no al revés.
Lectura adicional
- Punto de reorden, cómo se aplican los cuantiles a la optimización del inventario.
- Función de pérdida pinball, cómo medir la precisión de un pronóstico cuantílico.
- Roger Koenker, Kevin F. Hallock, (2001) Quantile Regression, Journal of Economic Perspectives, 15 (4), 143–156
- Ichiro Takeuchi, Quoc V. Le, Timothy D. Sears, Alexander J. Smola, (2006), Nonparametric Quantile Estimation, Journal of Machine Learning Research 7 1231–1264
