Главная »
Ресурсы » Здесь
Математическое распределение — это мощная и полезная модель для многих ситуаций, особенно при наличии неопределенностей. ‘'Распределение
— важнейшая функция в языке Envision, который поддерживает широкий спектр связанных с ней операций. Все вместе эти операции в Envision называются алгеброй распределения
. В данном разделе мы рассмотрим типы данных для распределения, а также операторы и функции, которые применяются к ним.
Типы данных для распределения
Математическое распределение представляет собой объект, который обобщает понятие функции. Цель Envision гораздо скромнее: такие объекты по сути представляют собой функции $f: \mathbb{Z} \to \mathbb{R}$. Мы называем эти (математические) функции распределением
, потому что в Envision они чаще всего используются для обработки распределения вероятностей
, то есть чаще всего используется строго положительное распределение с массой 1.
Распределение в Envision материализовано в виде особого типа данных, который называется распределение
. Другие типы данных — это число
и текст
. Данные типа «распределение» работают достаточно сложно, и это объясняется тем, что они представляют собой функции, а не отдельные значения. Например, ниже мы создаем дельта-функцию — дискретную функцию, равную 0 во всех точках, кроме 42, где она равна единице.
d := dirac(42)
Распределение можно экспортировать в файл с расширением ion. Однако распределение нельзя экспортировать в формат CSV или Excel как есть
.
В Envision существуют и другие способы создания функции распределения. Мы рассмотрим их в следующих разделах.
Графическое представление распределения
Распределение можно визуализировать с помощью гистограмм . Возьмем простое распределение Пуассона:
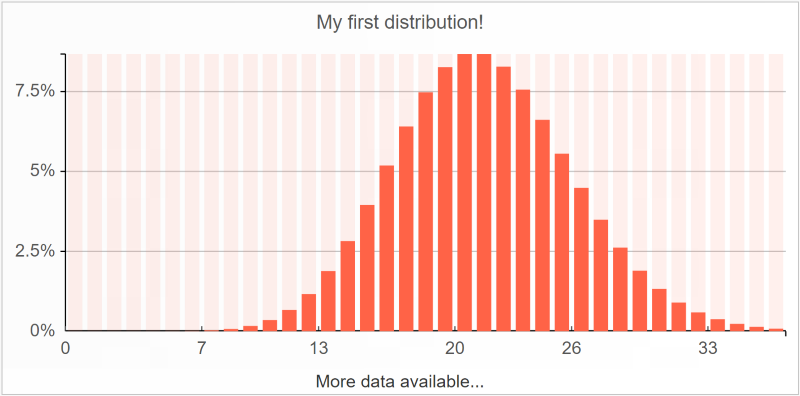
Данный график создан в Envision с помощью одной строчки кода, показанной ниже:
show histogram "My first distribution!" tomato with
poisson(21)
Использование ячейки histogram подразумевает, что после ключевого слова with должно быть единое скалярное распределение.
Точечные операции
Самые простые операции распределения — точечные
операции. Например, пусть $f$ и $g$ представляют собой две функции распределения $\mathbb{Z} \to \mathbb{R}$. Таким образом, мы можем выразить операцию сложения так:
$$f+g: k \to f(k) + g(k)$$
С точки зрения Envision, если X и Y — это векторы распределения, то та же самая операция будет выражена следующим образом:
Z = X + Y
Нужно отметить, что даже при работе с функциями распределения Envision остается векторным
языком. Из-за этого мы обычно не обрабатываем по одной функции распределения за раз, но весь вектор распределения сразу. Ту же самую операцию можно выполнить со скалярной точки зрения по следующей формуле:
Z := X + Y
В этом и следующих разделах мы используем в сценариях переменные X и Y как фактическое распределение.
Тогда точечное умножение и вычитание выражаются следующим образом:
$$f \times g: k \to f(k) \times g(k)$$
$$f-g: k \to f(k)-g(k)$$
Эти формулы можно легко преобразовать в синтаксис Envision:
Z = X * Y
Z = Z - Y
Если число $\alpha$ может быть воспринято как постоянная функция $f_{\alpha}: k \to \alpha$, то Envision позволяет комбинировать числа и функции распределения, но только при условии, что в результате получится компактная функция распределения.
// допустимо, компактная функция
Z = 2 * X
// нет деления на ноль — допустимо
Z = X / 2
// недопустимо, некомпактная функция распределения
Z = X + 1
// недопустимо, Y — компактная функция, а значит, она может быть равна нулю
Z = X / Y
Распределения также могут сдвигаться. Оператор сдвига обычно записывается так:
$$f_{n}: k \to f(k+n)$$
Синтаксис Envision для данной функции выглядит так:
Z = X << n // левый сдвиг
Z = X >> n // правый сдвиг
Если n является отрицательным числом, то операторы сдвига будут работать, но левый сдвиг становится правым и наоборот.
Создание функций распределения
Функции распределения можно создавать по-разному. Система прогнозирования Lokad создает функции распределения для времени выполнения заказов или спроса в будущем. После преобразования этих функций распределения в решетку (*) можно восстановить функцию распределения через функцию distrib(). Можно использовать следующий синтаксис:
Demand = distrib(Id, G.Probability, G.Min, G.Max)
Полученная переменная Demand представляет собой функцию распределения. Если исходная решетка содержит сегменты длиннее 1, функция distrib() равномерно распределяет массу по всему сегменту. Масса распределения сохраняется функцией distrib().
(*) Сериализация функции распределения — это процесс превращения данных распределения в обычную таблицу, которую можно хранить в виде простого файла. Для работы с функцией распределения как таковой (а не как с таблицей) нужно произвести обратную сериализацию таблицы. В сценарии выше это выполняется с помощью функции distrib().
Кроме того, Envision дает возможность создать функцию распределения непосредственно из набора полученных числовых значений. Для этого используется агрегатор ranvar():
X = ranvar(Orders.Quantity)
Агрегатор ranvar() возвращает случайное значение
, которое совпадает с частотой, обнаруженной в группе агрегации. Если данных для объединения недостаточно, ranvar() возвращает dirac(0).
Наконец, можно создать распределение из временных рядов
с помощью агрегатора ranvar.segment().
D = ranvar.segment(
// первая дата для каждого элемента
start: Items.Start
// последняя дата для каждого элемента (включительно)
end: Items.End
// длительность периода для каждого элемента
horizon: Items.Horizon
// целое число для пропущенных элементов
step: Items.Step
// дата для каждого события
date: Orders.Date
// количество для каждого события
quantity: Orders.Quantity)
Для каждого элемента рассчитывается распределение суммы объемов по периодам с горизонтами от первой до последней даты для соответствующего элемента. Как правило, длительность горизонта соответствует времени выполнения заказа для соответствующего элемента.
Разложение распределения в таблице
В предыдущем разделе мы увидели, как можно объединять данные таблицы и создавать распределение. Можно выполнить и обратный процесс, то есть разложить распределение по строкам таблицы. В данном разделе мы рассмотрим функцию extend.distrib(), которая выполняет данную задачу. Синтаксис данной функции выглядит так:
X = poisson(1)
table G = extend.distrib(X)
G.Probability = int(X, G.Min, G.Max)
show table "My Grid" with
Id
G.Min
G.Max
G.Probability
Где X — вектор распределения, заданный в строке 1 как распределение Пуассона. В строке 2 данные распределения включаются в таблицу с названием G («Решетка»). Эта таблица привязана к (Id, *), и, как видно из строк 3–7, таблица также автоматически заполняется числовыми значениями в столбцах G.Min и G.Max. Значения G.Min и G.Max представляют собой допустимые предельные значения.
При разложении сравнительно компактного распределения таблица обычно состоит из строк, различающихся на 1 единицу (то есть от G.Min до G.Max с шагом +1 между соседним строками). Тем не менее, если бы нам пришлось выполнять разложение распределения при большом количестве значений, например dirac(1000000), то создавать таблицы из миллиона строк было бы крайне неэффективно. Именно поэтому функция extend.distrib() объединяет данные большого распределения в группы. Для этого и нужны допустимые предельные значения групп G.Min и G.Max.
Для большего контроля за детализацией таких групп функция extend.distrib() позволяет использовать первую перегрузку:
table G = extend.distrib(X, S)
Где S представляет собой числовой вектор. В результате в таблице отражаются группы, соответствующие сегментам [0;0] [1;S] [S+1; S+M] [S+M+1;S+2*M] ..., где M является размером группы по умолчанию (также называется коэффициентом
). Данная перегрузка часто используется, когда нужно учесть уровень спроса, который выше общего запаса
.
Наконец, вторая перегрузка extend.distrib() дает еще больший контроль:
table G = extend.distrib(X, S, M)
Где M — обязательный размер группы. Если M равен нулю, то при разложении используется размер группы по умолчанию, который настраивается Envision автоматически. Вторая перегрузка очень полезна при использовании коэффициентов партий
при размещении заказов, так как спрос нужно сопоставить с партиями определенного размера.
Помните, что extend.distrib(X, S, M) может выдать ошибку из-за ограничений вашей учетной записи Lokad, если вы попытаетесь разложить большое распределение при малом коэффициенте партий.
Свертка распределения вероятности
Свертка — это сложная операция, применяемая в функциях распределения. В основном такие операции используются для случайных переменных
. В отличие от точечных операций свертка позволяет выполнять такие операции, как сложение или умножение независимых случайных переменных. Свертки в Envision состоят из двух символов и оканчиваются на *, например:
// свертка сложения
Z = X +* Y
// свертка вычитания; то же самое, что X +* отриц. (Y)
Z = X -* Y
// свертка умножения
Z = X ** Y
// свертка показателя степени
Z = X ^* Y
Свертка сложения (и вычитания) может быть представлена в виде суммы (разности) двух независимых случайных переменных $X+Y$ (или $X–Y$). Свертка умножения, также известная как свертка Дирихле, может быть представлена как произведение двух независимых случайных переменных.
Порядок свертки более сложен и представляет собой следующие расчеты:
$$X ^ Y = \sum_{k=0}^{\infty} X^k \mathbf{P}[Y=k] \text{ where } X^k = X + \dots + X \text{ ($k$ times)}$$
Последняя операция особенно интересна из-за связи с процессом, ведущим к интегрированному прогнозированию спроса, где $X$ представляет собой ежедневный спрос (предположительно постоянный), а $Y$ — вероятное время выполнения заказа.
См. статью о порядке свертки.
Историческая справка
Система прогнозирования Lokad начала работать с квантильными схемами
в начале 2015 г. Эти схемы не были непосредственным
представлением распределения вероятности тех или иных событий (это были просто интерполированные квантильные прогнозы), но мы все ближе подходили к распределению. Работая с клиентами, мы начали понимать, какой огромный потенциал заключен в анализе вероятностей, если применять его для количественной оптимизации цепей поставок. Наши решетки
представляли собой большие таблицы, в которых была отражена вероятность всех событий. И хотя эти решетки и были прорывом как для клиентов, так и для нас самих, мы быстро осознали, что обработка вероятности событий, представленных в виде списка, отнимает много времени и сил.
Под «алгеброй распределения» понимается широкий набор технологических наработок Lokad для решения проблемы неопределенности будущего в цепях поставок. Для работы с указанными ситуациями требуется не просто среднестатистический прогноз, но полноценный анализ рисков с учетом всех возможных вариантов развития событий. В основе Envision лежит идея о том, что необходимо рассматривать все варианты
, а не только немногие специально отобранные. С этой целью в сценарии Envision вводятся случайные величины, которые обрабатываются с помощью соответствующих операций, таких как свертки'’ — более подробное описание приводится далее. На практике алгебра распределения представляет собой элегантный способ моделировать сложных ситуаций в цепях поставок, когда ни спрос, ни время выполнения заказа в будущем не могут быть четко определены.
