Pinball 损失函数(分位数准确度)
首页 » 知识库 » 此处
作者:Joannes Vermorel,2012 年 2 月
评估分位数预测是一个很微妙的问题。传统预测的目标是使预测尽量接近观察值,与之相比,分位数预测的确会(有意)出现偏差。因此观察值与预测值的比较不尽如人意。借助 pinball 损失函数将返回可解释为分位数预测模式准确度的值。
公式
假设 $\tau$ 为目标分位数,$y$ 为实际值,$z$ 为分位数预测,则 pinball 损失函数 $L_\tau$ 可以这样编写:$$ \begin{eqnarray} L_{\tau}(y,z) & = & (y - z) \tau & \textrm{ if } y \geq z \\\ & = & (z - y) (1 - \tau) & \textrm{ if } z > y \end{eqnarray} $$
下载: pinball-loss-function.xlsx
该电子表格说明了如何在 Microsoft Excel 中计算 pinball 损失函数。实际公式并不比 MAPE 等大部分准确度指标复杂。
示例
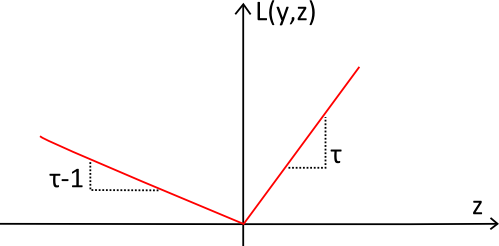
pinball 损失函数(红色)根据球体弹到 pinball 上时的轨迹形状命名。这种函数始终为正,$L_\tau(y,z)$ 的值越大,就越是偏离目标 $y$。斜率用于体现分位数预测中预期的不稳定性。
pinball 损失最小的最佳分位数模式
与 pinball 损失函数相关的结果最重要的就是pinball 损失越小,分位数预测越准确。Pinball 损失最小的函数所提供的分位数预测最佳,这一点是可以证明的。但本文不会对证明这一点所需采用的形式进行介绍。
如要比较两种分位数模式(例如 Lokad 与其他模式)相应的准确度,只要计算每种模式在范围足够大的时序内的平均 pinball 损失,保证所观察到的差异具有统计意义就足够了。在实践中,只要数百个时序便足以评估哪种分位数模式最准确。
Lokad 的洞察
在我们看来,传统预测(即平均数预测)简单的准确度理念被过高估计了。平均数和分位数之类的预测被过度拟合,导致预测模式的比较变得异常复杂。但是,pinball 损失函数为评估两种分位数预测模式的相对准确度提供了一种相当简单的途径。参考文献
- 连续分位数预测时序,2011 年 3 月,作者:Gerard Biau 和 Benoit Patra,Information Theory, IEEE Transactions
- 连续概率排位分数 (CRPS),即 Pinball 损失函数针对概率预测的泛化