利用销售预测计算安全库存
首页 » 知识库 » 此处
作者:Joannès Vermorel,2007 年 12 月(上次修订时间:2012 年 1 月)
下文介绍的方法是有着数十年之久的传统方法,但 Lokad 近期在分位数预测方面的发展使得这种安全库存模式在一定程度上过时了。再订货点实际上就是分位数预测。平均说来,直接计算分位数的表现远超安全库存模式所提供的间接计算。
本指南阐述了如何通过将安全库存调整到最佳水平来优化库存。本指南适用于零售业和制造业。其中的理论通过 Microsoft Excel 说明。对于想将该理论引入定制应用的软件开发人员,我们还提供了高级说明。目标受众:本文档主要面向零售业或制造业中的供应链专员,但对于希望使用库存管理功能来扩展应用的会计 /ERP /电子商务软件编辑人员,本文同样实用。
我们已力求减少对数学方面的要求,但我们无法做到避免所有公式,因为本文档的用途正是作为一种说明如何计算安全库存的实用指南。
下载: calculate-safety-stocks.xls (Microsoft Excel 表)
简介
库存管理是库存成本与缺货成本之间的金融取舍。库存越多,所需的流动资金越多,存货跌价的风险越高。另一方面,如果存货不足,那么就会发生库存缺货,导致与潜在的销售机会失之交臂,甚至可能中断整个生产流程。存货实质上取决于两个因素:
这两个因素受各种不确定性的影响
- 需求变化:客户行为可能以无法预测的方式演变。
- 交付周期变化:供应商或承运人可能面临各种计划外的问题。
确定安全库存量相当于考虑各种不确定性来对这些成本进行取舍。
对存货成本与缺货成本的权衡高度依赖于业务。因此,现在我们不会直接考量这些成本,而是要引入服务水平的概念。
服务水平表示特定水平的安全库存不会导致缺货的概率。自然而言,安全库存提高,服务水平随之相应提高。当安全库存极高时,服务水平会接近于 100%(即发生缺货的概率为 0)。
选择服务水平(即可接受的缺货概率)不在本指南的范畴之内,但关于计算最佳服务水平,我们提供了独立的指南。
库存补货模式
运用我们的库存预测 技术可获得经过优化的安全库存。Lokad 精通于通过需求预测来优化库存。我们的预测引擎工具涵盖本指南中所涉及的功能及其他许多原生功能。
再订货点即触发订单的库存量。如果不存在任何不确定性(即完全清楚未来的需求且供应链绝对可靠),那么再订货点就是交付周期(也称为交付周期需求)中总的预测需求。
Lokad 提供了多种工具用来根据历史数据直接计算交付周期需求。请参阅基于 Excel 的预测方法和公式。
在实践中,由于存在种种不确定性,因此
再订货点 = 交付周期需求 + 安全库存假设预测无偏差(从统计的角度看),那么安全库存为零将导致服务水平为 50%。实际上,无偏差预测意味着未来需求大于或小于交付周期需求的可能性很高(请记住,交付周期需求只是预测的值而已)。
注意:即使预测没有确切的值,也有可能没有偏差。偏差表示预测模式的系统误差(例如:需求总是高估 20%)。
误差的正态分布
在这里,我们需要采用一种途径来展示交付周期需求中的不确定性。在下文中,我们将假设误差呈正态分布,请参见下图。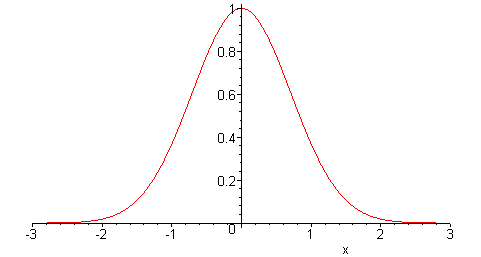
统计说明:这种正态分布假设并非完全任意。在某些情况下,统计估值收敛为正态分布,如中心极限定理中所述。但本指南中不会考虑这些因素。
正态分布仅由两个参数定义:平均数和方差。由于假设了预测无偏差 - 我们假定误差分布的平均数为零,但这并不说明误差也假设为零。
确定预测误差的方差是一项较难处理的工作。为此,和大部分预测工具套件一样,Lokad 也提供了与预测相关的MAPE 估计(平均绝对百分误差)。为了完整起见,我们将说明如何使用简单的直观推断来解决这一问题。
历史数据中的方差可以作为一种良好的直观推断来估计预测误差方差。David Piasecki 也建议不使用方差表达式中的平均需求,而是使用预测的需求,即
σ2 = E[ (yt - y')2 ]其中
E 为求平均数运算符,yt 为周期 t 的历史需求(通常为销售量),y' 为预测的需求。这一假设蕴含的主要原理在于预测误差往往与预计的变化量有关:即将发生的变化越大,预测中的误差越大。
实际上,计算误差方差涉及到一些细微之处,对此将在下文详细说明。
安全库存表达式
至此,我们已确定了平均数和方差,因此误差分布是已知的。现在必须计算这种分布中可接受的误差水平。在上面我们已经引入了服务水平(百分比值)的概念来实现这个过程。备注:尽管我们假设的是静态的交付周期,但对于变化的交付周期,同样可以采用非常形似的方法。
要将服务水平转化为误差水平(也称为服务系数),必须使用逆累积正态分布(有时也称为“逆正态分布”)(有关相应的 Excel 函数,请参见 NORMSINV)。这听起来有点复杂,所以建议您查看正态分布 Java 小程序以进行直观了解。如您所见,累积函数可将百分比转化为曲线下方的面积,X 轴阈值对应于服务系数值。
从直观上,安全库存的计算公式为
安全库存 = 误差的标准差 * 服务系数假设
S 为安全库存,可以得到S = σ * icdf(P) 其中
σ 为标准差(即上面定义的方差 σ2 的平方根),cdf 为规范化的累积正态分布(平均数为 0 且方差等于 1),P 为服务水平。请记住
再订货点 = 交付周期需求 + 安全库存 假设
R 为再订货点,可以得出R = y' + σ * icdf(P)匹配交付周期与预测周期
至此,我们假设了对于给定的交付周期,可以直接生成相应的未来需求预测。但在实践中,并非完全以这种方式运作。分析历史数据通常从将数据聚合成周期开始(一般按周或按月)。但是,选定的周期可能不完全匹配交付周期;所以需要通过进一步的计算来表现交付周期需求及其相关变化(考虑到我们仍假设预测误差呈正态分布,如上一节中所述)。
直观地说,交付周期需求可以作为与交付周期时段相交的未来周期的预测值之和。必须小心地正确调整上次预测的周期。
从形式上说,假设
T 为周期,L 为交付周期。可以得出L = k * T + α * T 其中
k 为整数,0 ≤ α < 1。
令 D 为交付周期需求,关于交付周期需求得到的最终表达式为D = (Σt=1..k y't) + αy'k+1 其中
y'n 为针对未来的第 n 个周期预测的需求。鉴于相同的正态分布假设,预测误差方差可以这样计算
σ2 = E[ (yt - y')2 ] 其中
y' 为根据周期的平均预测y'= D / (k + α)但是,这里计算的
σ2 是根据周期的方差,但我们需要的是匹配交付周期的方差。令 σL2 为调整后的根据交付周期的方差,可以得出σL2 = (k + α) σ2 最后,再订货点可以重新表示为
R = D + σL * cdf(P)利用 Excel 计算再订货点
本节详细介绍了如何利用 Microsoft Excel 计算再订货点。建议您先看一下所提供的 样本 Excel 表。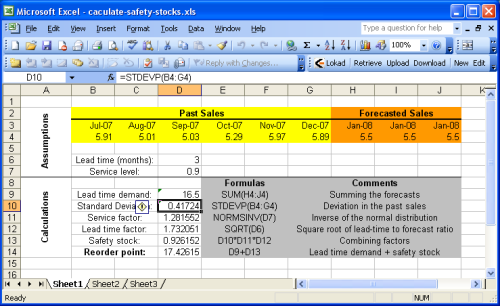
该样本表主要分为两部分:上面的部分为假设,下面的部分为计算。预测属于“假设”部分,因为销售(或需求)预测不在本指南的范畴之内。有关详细信息,请参考利用 Microsoft Excel 预测销售的指南。
上一节中说明的大部分公式是非常普通的运算(加法、乘法),这些运算利用 Microsoft Excel 可以非常方便地进行,但有两个函数要提一下
NORMSINV(Microsoft KB):估计累积正态分布,即上文中提到的cdf。STDEV(Microsoft KB):估计标准差,即上文中提到的σ。我们将标准差σ也称为方差σ2的平方根。
为了简单起见,第一个表在计算服务系数时没有实现对
σ2 = E[ (yt - y')2 ] 的直观推断。这种方法在 Sheet2( Excel 文档中的第 2 个表)中实现。由于本例中假设的是静态预测,因此无论有没有这种直观推断,再订货点都是相同的。开发人员注意事项
本节面向要对自动化库存管理实现补货功能的开发人员。本指南中的大部分公式可以简洁地通过常规开发工具实现。如果您使用碰巧在使用 .NET,建议您使用 Math.NET Iridium(这是一种用 C 语言编写的数学库,其中提供有标准差运算符和累积正态分布函数)。
另外,标准差也可以很容易地根据其定义重新实现,请参见维基百科页面。累积正态分布略微复杂,但 Peter J. Acklam 提供了一种优秀算法,这种算法已进行了多种语言的实现。这两种方法需要的代码只有几十行。