Algebra delle distribuzioni

Le distribuzioni matematiche sono un potente strumento, utile a elaborare modelli per molte situazioni commerciali, soprattutto quelle che prevedono una certa dose di incertezza. Envision tratta le distribuzioni "con i guanti" e ne sfrutta il potenziale per gestire le situazioni più diverse. L'insieme delle operazioni di questo tipo supportate da Envision viene da noi definito come algebra delle distribuzioni. In questa sezione, vedremo in dettaglio in cosa consistono le distribuzioni e quali sono gli operatori e le funzioni a esse applicabili.

I dati di tipo distribuzione    Schematizzare una distribuzione    Operazioni punto per punto    Generare le distribuzioni    Estendere una distribuzione in una tabella    Convoluzioni delle distribuzioni di probabilità    Cenni storici

I dati di tipo distribuzione

In matematica, le distribuzioni sono oggetti che generalizzano il concetto di funzione. Con Envision, il nostro intento è ben più modesto: quelle che chiamiamo distribuzioni sono in realtà funzioni matematiche $f: \mathbb{Z} \to \mathbb{R}$. Ci riferiamo a queste funzioni con il termine distribuzioni perché Envision è utilizzato soprattutto per gestire distribuzioni di probabilità, ossia distribuzioni essenzialmente positive con massa pari a 1.

In Envision, le distribuzioni si manifestano attraverso un particolare tipo di dati, denominato distribuzione. Altri tipi di dati sono numero o testo. I dati di tipo distribuzione hanno comportamenti relativamente complessi, proprio perché sono funzioni e non valori singoli. Nell'esempio qui sotto, generiamo una funzione delta di Dirac, ossia una funzione discreta con un valore 0 ovunque, meno che al punto 42, dove il valore è 1.

d := dirac(42)

Le distribuzioni possono essere esportate in un file di dati Ionic, oppure, direttamente così come sono in file CSV o Excel.

Envision offre comunque molti altri modi di generare distribuzioni, che vedremo più avanti.

Schematizzare una distribuzione

Le distribuzioni possono essere rappresentate con istogrammi. Consideriamo una semplice distribuzione di Poisson:



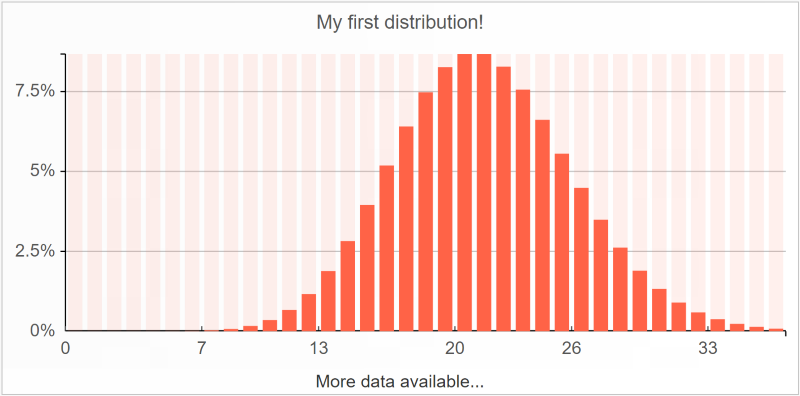
L'immagine sopra è stata generata da Envision con la seguente riga di script:

show histogram "My first distribution!" tomato with poisson(21)

La casella histogram (istogramma) si aspetta di trovare, dopo la parola chiave with, una distribuzione scalare singola.

Operazioni punto per punto

Le operazioni più semplici che si possono eseguire con le distribuzioni sono dette operazioni punto per punto. Ad esempio, date $f$ e $g$, che rappresentano le due distribuzioni $\mathbb{Z} \to \mathbb{R}$, possiamo definire l'addizione come:

$$f+g: k \to f(k) + g(k)$$ Nell'ottica di Envision, ipotizzando che X e Y siano vettori di distribuzione, la stessa operazione può essere scritta in modo simile come:

Z = X + Y

È importante sottolineare che, anche quando lavoriamo con le distribuzioni, Envision rimane pur sempre un linguaggio basato su vettori, per cui non elaboriamo una sola distribuzione alla volta, ma un intero vettore di distribuzioni alla volta. La stessa operazione può essere eseguita in prospettiva scalare usando

Z := X + Y

In questa e nelle sezioni successive, ogni volta che usiamo X e Y negli esempi di script, ipotizziamo che le due variabili siano distribuzioni vere e proprie.

La moltiplicazione e la sottrazione punto per punto sono allora definite con: $$f \times g: k \to f(k) \times g(k)$$ $$f-g: k \to f(k)-g(k)$$ che si traducono in modo piuttosto trasparente nella sintassi di Envision seguente:

Z = X * Y
Z = Z - Y

Partendo dal presupposto che $\alpha$ può essere implicitamente assimilata a una funzione costante $f_{\alpha}: k \to \alpha$, Envision consente di combinare numeri e distribuzioni, a condizione che la distribuzione risultante sia compatta.

// corretto, è compatta
Z = 2 * X 
// è corretto non dividere per zero
Z = X / 2 
// sbagliato, non è compatta
Z = X + 1 
// sbagliato, Y è compatta e ha quindi valori nulli
Z = X / Y 

Le distribuzioni possono anche essere sottoposte a shift. L'operatore di shift viene di solito scritto come:

$$f_{n}: k \to f(k+n)$$ La sintassi Envision corrispondente è:

Z = X << n // shift a sinistra
Z = X >> n // shift a destra

Ovviamente, se n è negativo, allora l'operatore di shift funzionerà lo stesso, ma lo shift a destra diventerà uno shift a sinistra, e viceversa.

Generare le distribuzioni

Esistono diversi modi per generare una distribuzione: il motore di previsione di Lokad genera distribuzioni al fine di prevedere i lead time futuri o la domanda futura. Se queste distribuzioni sono state ordinate in una serie contenuta in una tabella (*), è possibile generare di nuovo la distribuzione attraverso la funzione distrib(). La sintassi corrispondente è:

Demand = distrib(Id, G.Probability, G.Min, G.Max)

La variabile risultante Demand (domanda) è una distribuzione. Se la tabella originale include segmenti più lunghi di 1, distrib() ripartisce la massa in maniera uniforme in tutto il segmento. La massa della distribuzione viene mantenuta dalla funzione distrib().


Envision offre inoltre la possibilità di generare una distribuzione direttamente da un set di valori numerici osservati, utilizzando l'aggregatore ranvar():

X = ranvar(Orders.Quantity)

L'aggregatore ranvar() restituisce una variabile casuale che corrisponde alla frequenza osservata nei gruppi di aggregazione. Quando non ci sono dati da aggregare, ranvar() restituisce dirac(0).

Infine, è possibile generare una distribuzione da serie temporali, utilizzando l'aggregatore ranvar.segment().

D = ranvar.segment(
// prima data per ogni articolo
start: Items.Start 
// ultima data (compresa) per ogni articolo
end: Items.End 
// lunghezza del periodo per ogni articolo
horizon: Items.Horizon 
// numero intero per saltare gli elementi
step: Items.Step 
// data corrispondente a ogni singolo evento
date: Orders.Date 
// quantità per ogni singolo evento
quantity: Orders.Quantity) 

Per ogni articolo, viene calcolata la distribuzione della somma delle quantità corrispondenti all'evento per i periodi con una lunghezza di orizzonte compresa interamente tra la prima e l'ultima data disponibile per l'articolo analizzato. La lunghezza dell'orizzonte corrisponde solitamente al lead time dell'articolo.

Estendere una distribuzione in una tabella

Nella sezione precedente abbiamo visto come aggregare una tabella in una distribuzione, ma è anche possibile il processo inverso, quello cioè di estendere una distribuzione in una tabella. In questa sezione vedremo come fare, con l'aiuto della funzione extend.distrib(), il cui scopo è proprio questo. La sintassi è illustrata qui di seguito:

X = poisson(1)
table G = extend.distrib(X)
G.Probability = int(X, G.Min, G.Max)
show table "My Grid" with 
Id
G.Min
G.Max
G.Probability

dove X è il vettore di distribuzione generato alla riga 1 come distribuzione di Poisson. Alla riga 2, le distribuzioni sono inserite in una tabella denominata G (da "griglia"). La tabella ha un'affinità (Id, *) e, come si vede alla riga 3, la tabella viene popolata automaticamente con le colonne numeriche G.Min e G.Max. Sia G.Min che G.Max sono estremi inclusivi.

Quando vengono estese distribuzioni relativamente compatte, la tabella risultante contiene di solito righe che presentano un incremento pari a 1 (G.Min e G.Max aumentano cioè di 1 unità da una riga all'altra). Tuttavia, se consideriamo l'estensione di distribuzioni con valori elevati, ad esempio dirac(1000000), sarebbe controproducente generare una tabella con milioni di righe. In questo ci viene in aiuto la funzione extend.distrib(), che aggrega le distribuzioni più grandi in gruppi più compatti. Questo spiega perché gli estremi inclusivi del gruppo sono rappresentati sia da G.Min che da G.Max.

Per un maggiore controllo sulla granularità di questi gruppi, la funzione extend.distrib() offre un primo sovraccarico:

table G = extend.distrib(X, S)

dove S è un vettore numerico. La tabella che ne risulta mostra gruppi allineati ai segmenti [0;0] [1;S] [S+1; S+M] [S+M+1;S+2*M] ... dove M è la dimensione predefinita del gruppo, detta anche moltiplicatore. Questo sovraccarico è tipico delle situazioni in cui è necessario considerare una domanda superiore alle scorte totali.

Il secondo sovraccarico di extend.distrib() consente un controllo ancora maggiore con:

table G = extend.distrib(X, S, M)

dove M rappresenta le dimensioni obbligatorie del gruppo. Se M è pari a zero, allora l'estensione torna alla dimensione predefinita del gruppo, regolata automaticamente da Envision. Il secondo sovraccarico è particolarmente utile in caso siano presenti moltiplicatori di partite, poiché in queste situazioni la domanda deve essere compressa in gruppi di dimensioni specifiche.

È importante notare che usare extend.distrib(X, S, M) potrebbe non funzionare, a seconda delle capacità di calcolo associate al proprio account Lokad, quando si prova a estendere una distribuzione con valori elevati forzando un moltiplicatore basso.

Convoluzioni delle distribuzioni di probabilità

Le convoluzioni rappresentano una categoria di operazioni avanzate sulle distribuzioni. Le convoluzioni riguardano soprattutto le variabili casuali. A differenza delle operazioni punto per punto, le convoluzioni hanno interpretazioni probabilistiche, come la somma o la moltiplicazione di variabili casuali indipendenti. Envision riconosce le convoluzioni dagli operatori a due caratteri che terminano per *, come:

// somma di convoluzione
Z = X +* Y 
// differenza di convoluzione, come X +* reflect(Y)
Z = X -* Y 
// prodotto di convoluzione
Z = X ** Y 
// potenza di convoluzione
Z = X ^* Y 

La somma di convoluzione (e, allo stesso modo, la differenza di convoluzione) può essere interpretata come la somma (o la differenza) di due variabili casuali indipendenti $X+Y$ (o $X-Y$). Il prodotto di convoluzione, noto anche come convoluzione di Dirichlet, può essere interpretato come il prodotto di due variabili casuali indipendenti.

La potenza di convoluzione è più complessa e rappresenta: $$X ^ Y = \sum_{k=0}^{\infty} X^k \mathbf{P}[Y=k] \text{ dove } X^k = X + \dots + X \text{ ($k$ volte)}$$ Quest'ultima operazione è quella che ci interessa di più, poiché è legata al processo di previsione integrata della domanda, dove $X$ rappresenta la domanda quotidiana (che presumiamo sia stazionaria) e $Y$ rappresenta il lead time probabilistico.

Vedere anche la nostra pagina dedicata alla potenza di convoluzione.

Cenni storici

All'inizio del 2015, il motore di previsione di Lokad ha iniziato a offrire le prime previsioni con le tabelle dei quantili: si trattava semplicemente di previsioni con quantili interpolati, non di distribuzioni di probabilità vere e proprie, ma eravamo già a buon punto. Lavorando fianco a fianco con i nostri clienti, ci eravamo resi conto già allora dell'enorme potenziale dell'analisi probabilistica applicata all'ottimizzazione quantitativa della catena logistica. Le nostre tabelle, però, non erano altro che enormi liste di probabilità e, poiché si trattava di una novità assoluta sia per i clienti che per noi stessi, non ci abbiamo messo molto a capire che elaborare delle probabilità presentate sotto forma di liste era piuttosto complesso.

L'algebra delle distribuzioni è la risposta tecnologica di Lokad alle sfide logistiche che implicano scenari futuri ignoti: per affrontare tali sfide, infatti, non basta una singola previsione mediana, ma un'analisi di rischio completa, che prenda in esame tutte le evoluzioni possibili. Envision parte dal presupposto che sia necessario valutare tutti gli scenari, non solo quelli che sembrano più sensati. A questo proposito, è possibile inserire negli script Envision delle variabili casuali, che possono poi essere manipolate attraverso operazioni specifiche, denominate convoluzioni (su questo torneremo più avanti in dettaglio). A livello pratico, l'algebra delle distribuzioni è un modo elegante per modellare situazioni complesse dal punto di vista logistico, in cui sia la domanda futura che il lead time futuro sono ignoti.