QUANTILE TECHNOLOGY PART I
Regarder sur YouTube.
QUANTILE TECHNOLOGY PART II
Regarder sur YouTube.
Gestion des stocks de pièces détachées avec les quantiles (PDF)
Dans un monde où la plupart des fabricants d'équipements et des distributeurs opérent sur des marchés terriblement compétitifs, pourvoir fournir à sa clientèle un taux de service élevé est une priorité stratégique pour beaucoup d'entreprises. Cependant, gérer des stocks de pièces détachées de façon efficace reste un défi énorme du fait des volumes et de la nature erratique de la demande. Ce livre blanc aborde ce problème, ainsi que l'état de l'art en termes de technologie de planification pour les pièces détachées. Il introduit également la notion de prévision quantile comme une nouvelle approche révolutionnaire pour aborder ce problème.
Le terme de prévision quantile peut paraître compliqué, et, à moins que vous soyez un expert en statistiques, il est possible que vous ne l'ayez encore jamais rencontré. Cependant, des prévisions quantiles sont utilisées régulièrement par les distributeurs et fabricants – sans pour autant être connues sous ce nom. Par exemple, définir un point de commande pour vos stocks équivaut strictement à générer une prévision quantile sur la demande.

Malgré l'impact radical que peuvent avoir les prévisions quantiles dans la distribution et la fabrication, les quantiles ont reçu peu d'attention dans ce domaine jusqu'à présent. L’explication la plus simple en est que le support requis pour des prévisions quantiles était quasiment inexistant dans le secteur logiciel. Cependant, avec Lokad, il n'y a plus de raison de négliger un aspect technologique aussi critique.
Pour comprendre pourquoi les prévisions quantiles sont utiles pour un distributeur ou un fabricant, nous devons tout d'abord revenir sur la raison pour laquelle les prévisions, de manière générale, sont nécessaires. Les prévisions de la demande sont critiques pour s'assurer que le bon niveau de ressources - tels que les stocks, les effectifs ou les liquidités - soit disponible au bon moment.
Cependant, fournir le bon niveau de ressources pour satisfaire la demande est généralement un problème très asymétrique: Le coût d’une sur-allocation de ressources (ou sur-prévision) peut grandement différer du coût d’une sous-allocation de ressources (ou sous-prévision).
Par exemple :Ainsi, pour les entreprises, il n’est généralement pas rentable d’alouer des ressources sur la base de prévisions moyennes brutes de la demande, étant donné qu'alouer trop peu de ressources à 50% du temps est un compromis assez médiocre, qui ne reflète pas la réalité des activités. Ainsi, les entreprises introduisent volontairement un biais dans leur allocation de ressources pour refléter l’asymétrie spécifique à leurs activités. Les prévisions quantiles permettent justement de mieux gérer cette asymétrie.
Définition : une prévision quantile (τ, λ), où τ est la probabilité cible, et où λ (lambda) est l’horizon exprimé en jours, représente une prévision de la demande sur les prochains λ jours, venant avec une probabilité de τ d'être supérieure à la demande future (et par conséquent, une rentabilité 1-τ d'être inférieure à la demande future).
Les prévisions quantiles existent depuis des décennies, cependant implémenter un modèle de prévisions quantiles natif est fréquemment, et à juste titre, considéré comme étant bien plus compliqué qu'implémenter un modèle de prévisions moyennes. Par conséquent, la grande majorité des éditeurs de logiciels de prévision (*) ne fournissent que des prévisions moyennes.
(*) A notre connaissance, Lokad est devenu, en mars 2012, le premier éditeur à fournir une technologie de prévisions quantiles native, à l'usage des entreprises. Cependant, dans les cercles académiques, la recherche de prototypes pour la régression quantile existe depuis des décennies.
Néanmoins, étant donné que les entreprises ont besoin de prévisions quantiles (qu'elles les connaissent ou non sous ce nom), elles contournent généralement le problème via l’extrapolation, afin de générer ces prévisions quantiles. D’un point de vue pratique, cette approche consiste à faire l'hypothèse que la demande suit une distribution normale, et à ajouter un terme de sécurité correcteur. A titre d'exemple, l’approche classique du stock de sécurité suit ce modèle.
Les quantiles extrapolés sont des prévisions (moyennes) classiques, transformées en prévisions quantiles grâce à une méthode d’extrapolation. Le terme est opposé aux quantiles natifs dans lesquels le modèle statistique produit directement le quantile. L’extrapolation ne repose pas sur les données d’entrée, mais plutôt sur une distribution définie a priori. Cette distribution - généralement la distribution normale - a tendance à être le maillon faible du processus d’extrapolation, car elle diffère de la réalité.
Malheureusement, l’extrapolation présente de gros inconvénients dans 3 contextes fréquents :
Dans ces situations, nous avons pu observer que les prévisions quantiles natives avaient tendance à dépasser de 20% ou plus les meilleures prévisions quantiles extrapolées ; la comparaison étant faite en exploitant les technologies de prévision quantiles et classiques de Lokad - ces dernières dépassant généralement elles-mêmes déjà celles de nos concurrents.
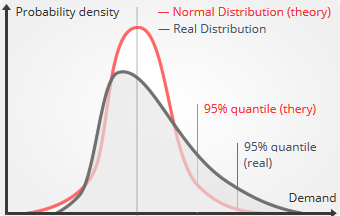
L’hypothèse selon laquelle les erreurs associées aux prévisions sont normalement distribuées est généralement bonne pour les quantiles ciblés proches de la moyenne ou de la médiane. Cependant, la qualité de l’ approximation se détériore à mesure que le pourcentage ciblé augmente. Pour les pourcentages cibles élevés - de façon générale pour toutes les valeurs supérieures à 90% -, nous avons constaté que l’extrapolation elle-même devenait fréquemment le maillon faible du processus de prévision. Dans ce cas, nous recommandons fortement de préférer les quantiles natifs.
L’extrapolation essaie de plaquer une courbe lisse sur la demande future afin de refléter l'incertitude. Cependant, lorsque la demande est intermittente ou "clairsemée" (sparse demand), elle n'a rien de lisse : pour chaque période (semaine, mois), le nombre d’unités vendues (i.e. la demande observable) est un nombre entier variant entre 0 et 5 par exemple.
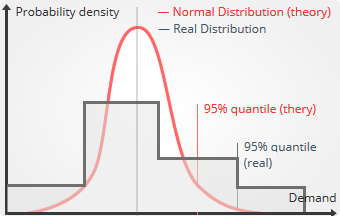
Historiquement, de nombreux modèles de prévision moyenne ont été conçus pour mieux appréhender la demande dite "clairsemée" ; cependant, sous l'angle des quantiles, il devient clair que le problème le plus fondamental est qu'aucune prévision moyenne ne peut être extrapolée correctement en un quantile précis en cas de demande clairsemée. A contrario, des quantiles natifs peuvent complètement s'adapter aux comportements la demande de type petits nombres entiers.
En cas de commandes groupées, la courbe de demande historique tend à présenter des pics. Ils reflètent le fait que quelques commandes clients représentent à elles seules un pourcentage significatif de la demande totale. Cependant, contrairement à la demande intermittente, il existe toujours en dehors de ces pics une demande non nulle. Le problème fondamental ici n'est pas que la demande ait des valeurs entières, mais que les prévisions de moyenne n'arrivent pas à projeter correctement ces pics dans le futur.
Pour simplifier, il existe deux approches pour gérer les pics :
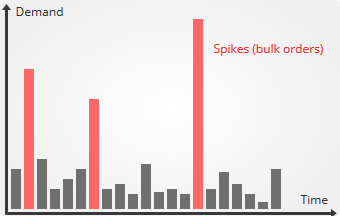
Dans les deux cas, les prévisions moyennes se comportent de façon assez médiocre : les quantiles extrapolés restent trop bas pour capturer ces pics, et dans le même temps, ils surestiment les ressources pour gérer la demande obtenue si l'on ignore ces pics. Les prévisions quantiles natives traitent les pics de manière plus directe et précise.
Lokad fournit un service en ligne complètement automatisé, qui prend des séries temporelles en entrée et renvoie des prévisions quantiles natives, chaque quantile correspondant à un horizon et un pourcentage cible (respectivement le délai de réapprovisionnement et le taux de service dans le cadre de l’optimisation des stocks). Aucune extrapolation n’est requise.
Le processus de prévision quantile ne nécessite aucune expertise en statistiques. En pratique, la plupart des entreprises utilisent notre application Web afin d’obtenir des points de commande optimisés ; le point de commande étant une prévision quantile spécifique aux stocks.
Pour chaque série temporelle, la prévision quantile est un simple point de données. Contrairement aux prévisions moyennes, les prévisions quantiles ne sont généralement pas représentées sous forme d'une courbe évoluant avec le temps et étendant la courbe historique dans le futur.
Les prévisions quantiles se comportent différemment, statistiquement parlant. Cependant les comportements fondamentaux sous-jacents de la demande restent les mêmes : tendance, saisonnalité, cycle de vie produit, promotions… Tous les comportements pris en charge par notre technologie de prévision classique sont également pris en charge par notre technologie de prévision quantile.
D’un point de vue mathématique, les prévisions quantiles représentent une généralisation de la notion classique de prévisions. D’un point de vue pratique, les prévisions quantiles sont généralement supérieures (en termes de précision) dans la plupart des cas où les risques associés à la sur-estimation et à la sous-estimation de la demande ne sont pas symétriques.
Cependant, les prévisions quantiles sont également moins lisibles et moins intuitives. Ainsi, les prévisions classiques restent un outil fondamental pour les managers, car elles leur permettent de mieux comprendre l’évolution de leur entreprise.
Nous ne nions absolument pas l'intérêt que peuvent avoir les prévisions classiques. En réalité, la majeure partie des efforts de R&D servant à développer notre technologie de prévision profitent aux deux types de prévisions. La prévision quantile nous permet d’affiner notre compréhension du comportement statistique de la demande. Notre priorité N°1, dans tous les cas, est de fournir des prévisions toujours plus précises.