クォンタイル回帰(時系列)
著者Joannès Vermorel、2012年2月推敲
クォンタイル回帰とは、故意に結果に偏りを導入する回帰の種類(すなわち予測)です。予測される変数の平均値を求める代わりに、クォンタイル回帰は中央値およびその他のクォンタイル(時によってはパーセンタイルとも称されます)を求めます。クォンタイルは再発注点を算出する直接手法であることから、在庫最適化に非常に有効です。
回帰とはここでは予測と同義語です。『予測』が結果による実用性を強調しているなら、『回帰』は数学的なアプローチを強調しています。
クォンタイル回帰の概念は、比較的先進的な統計上の話題です。この記事の目的は、この主題を厳格に扱うことではなく、小売業や製造業に携わる利用者に(比較的)直感的な導入をすることです。
クォンタイルの図解
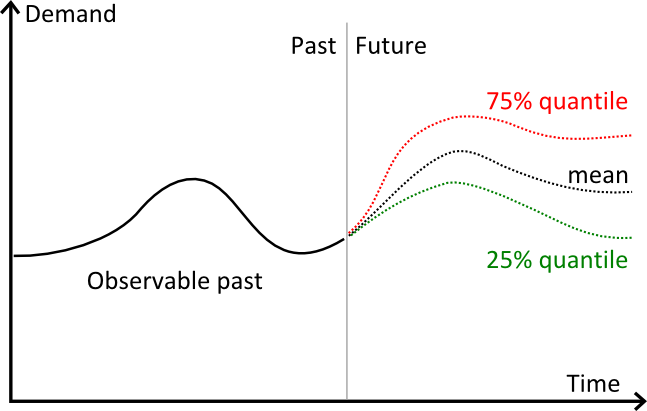
上のグラフは3つの別個の予測を示しています。
- 赤線が分位予測75%
- 黒線が平均値予測
- 緑線が分位予測25%
視覚的には、クォンタイルは信頼区間のような動きをします。しかし、実際にはクォンタイルは単一の目標割合のみに必要なのです。
将来の需要のクォンタイル(或いはパーセンタイル)
古典的な、最も直感的な予測は予測平均値です。過剰予測および過少予測のそれぞれの比重は同じでなければなりません。さもないと予測は偏ったものとなります(正確には平均値に対しての偏り)。確かに偏っていない予測は望ましい特性ですが、予測の精度については何も示していません。特に、予測というものは、偏っていないながら、同時に非常に不正確でもあるのです。偏りとは単に予測モデルが、将来の予測に対して上振れか下振れかの性向を示すに過ぎません。
この見方を洗練した最初のものが予測中央値となります。過剰予測と過小予測のそれぞれの頻度を等しいものとしなければなりません。さもなくば予測は中央値に対して偏っていることになります。
この段階で、既に偏っていない予測という概念を等しい比重から等しい確率に転換しています。この転換は僅かなものですが、状況によっては数値的に顕著な影響意を及ぼすものともなります。
実例:米国の家計収入の平均値 vs 中央値
家計収入は平均値および中央値の間の顕著な違いを示しています。米国国勢調査局によると、2004年の家計収入の中央値は$44,389であるが、同年の家計収入の平均値は$60,528となり、中央値を40%近く上回る数値となっています。
この差は他の人口に比べて非常に裕福な米国家庭の(比較上)高い所得によって説明されます。平均値と中央値の間の差は、対称ではない分布に見られます。一般に、正規分布に従わない全ての分布に言えることです。
中央値の一般化
中央値は、分布が50/50の確立に分割された時の閾値を表します。ただし、他の振動数比も考えられます。例えば、合計が100%となれば、80/20または90/10といった任意比率も考えられます。クォンタイルは任意の割合の中央値を一般化したものです。0から1の間の値となるτに対して、閾値よりも低い値となる確率が正確にτである時、クォンタイル回帰Q(τ)は閾値を表します。
分位予測
従来型予測も分位予測も、ともに入力は時系列時系列を取っています。時系列が入力データを示します。データに加えて、従来型の時系列平均値予測は2つの別の構造的設定が必要となります。- 日、週、月といった期間。
- 範囲。予測する期間の数を表す整数。
暗黙的に、期間によって時系列は集計され、実際に使うには十分に大きい場合、一般にリードタイムよりも大きい時に範囲が選ばれます。
平均値予測は非常に便利な特性の恩恵を受けます。数学的に予測を加算することは正しい のです。 例えばy1、y2、y3及びy4がこの先4週間の予測を表している場合、次の2週間の需要予測のみが必要となれば、y1+y2を合計すればよいのです。
一方で、クォンタイル予測を加算することは数学的には間違っています。より正確に言うならば、クォンタイルの合計で、(セグメントの合計)合計のクォンタイルが得られるわけではないのです。
クォンタイルを合計することができない理由をみてみましょう。スロットマシーンで毎週1ドルコイン遊ぶギャンブラーがいると想定してみましょう。50ドルの賞金を得る確率が1%、その他の賞金獲得率はゼロとしましょう。予想される賞金のクォンタイル99%を見ると、毎週、週に50ドルの賞金が得られることになります。しかし、二週間の期間で予想される賞金のクォンタイル99%を見ても、依然として50ドルです。二回賞金を獲得する確率は0.01%(1%掛ける1%)のみで、クォンタイル99%に変わりはないのです。週のクォンタイル99%を二つ合計すると100ドルとなりますが、実際にはクォンタイル99%が賞金を累計100ドル獲得するには10週必要です(この数値の結果の証明は、この記事の範囲を超えるため、ここでは記述しません)。
従い、クォンタイル予測は加算できず、クォンタイルの時系列予測は期間の集計という概念を改めて考慮しなければなりません。期間毎のクォンタイル予測を作成することは現実的に意味のないものです。セグメントの正しい分位値を生成する上で、基礎的予測を組み合わせることができないからです。
よって、クォンタイルの時系列予測は明瞭な構造を有しています。
- τ パーセンテージで示される目標クォンタイル
- λ 期間を示す範囲(通常日数)
例えば、時系列が商品Aの販売を示すとし、τ=0.90、λ=14日とした場合、クォンタイル予測(τ, λ)から、14日間で見られた需要総計よりも大きい需要の数値となる確率は正確に90%となります(同様に、同14日間で見られた需要総計よりも低い数値となる確率は10%)。
従来型予測と反対に、クォンタイル予測は一つ、範囲に関係なく、時系列毎に一つの数値しか出しません。ある意味、クォンタイル予測は従来型に比べて、期間の認識が不可能であるとも言えます。
Lokadのアプローチ
一見、クォンタイル予測は従来型に比べより複雑であるかのように思われます。しかし、現実世界では、一般に予測は正規分布に従うとの仮定の下で、クォンタイル予測として直ぐに外挿し予測するべく、最初の平均値予測を出す結果となります。ただ、外挿の段階は多くの場合、過程の最も脆弱な部分となり、最終結果が顕著に低下したものとなる可能性があります。予測技術は実用的な必要性に応じたものでなければなりません。つまり、本来のクォンタイル予測を出すべきと言えます。参考文献
- 再発注点:在庫最適化にどのようにクォンタイルが適用されるか。
- ピンボールロス機能:クォンタイル予測の精度の評価法。
- Roger Koenker, Kevin F. Hallock, (2001) クォンタイル回帰, Journal of Economic Perspectives, 15 (4), 143–156
- Ichiro Takeuchi, Quoc V. Le, Timothy D. Sears, Alexander J. Smola, (2006), Nonparametric Quantile Estimation(ノンパラメトリック分位点推定), Journal of Machine Learning Research 7 1231–1264