ピンボールロス機能（クォンタイル精度）


著者Joannès Vermorel、2012年2月推敲

クォンタイル予測の「精度」の評価は扱いにくい問題です。確かに、観察された値にできる限り近い値を予測するのが目標である従来型予測に対して、変位予測は（故意に）「バイアスがかかって」いる状況です。したがって、「観察された」VS「予測された」の単純な比較では満足できないわけです。ピンボールロス機能はクォンタイル予測モデルの「精度」として解釈される値に戻します。

公式

$\tau$ を目指す変位値、$y$ を実際の値、$z$ を変位予測、それから$L_\tau$ をピンボールロス機能とすると、以下のように表せます：

$$ \begin{eqnarray} L_{\tau}(y,z) & = & (y - z) \tau & \textrm{ if } y \geq z \\\ & = & (z - y) (1 - \tau) & \textrm{ if } z > y \end{eqnarray} $$

ダウンロード： pinball-loss-function.xlsx

スプレッドシートでは、マイクロソフト・エクセルでどのようにピンボールロス機能を計算するか説明しています。実際の公式は、MAPEなどのほとんど精度指標と同様に複雑なものではありません。

説明

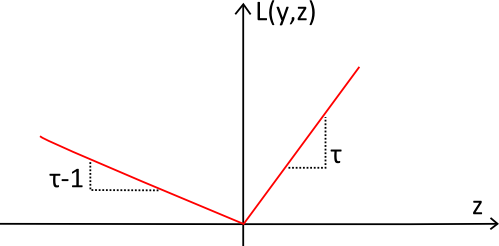
Graph of the Pinball loss function

ピンボールロス機能（赤で表示）は、ピンボールのボールの軌道にその形が似ていることから名づけられました。関数は常に正で、ターゲット$y$ から離れれば離れるほど、$L_\tau(y,z)$ 値が大きくなります。「傾斜」は変位予測において「望ましい不均衡」を示すのに使われます。

ベストな変位モデルはピンボールロスが最低となる

ピンボールロス機能に関連する結果で、最も重要なのはピンボールロスが低ければ低いほど、変位予測は正確になるということです。

ピンボールロスを最小化する関数は、最適変位値をも提供する、ということが証明可能です。しかし、証明についてはこの記事の範囲外となるので行いません。

したがって、二つの変位モデル（Lokad VS その他とでもしましょう。）のそれぞれの制度を比較するためには、観察される差異が統計的に有意な多数の時系列から、各モデルの「平均」を計算するだけで十分です。実際に査定するのは、変位モデルが最も「正確である」数百の時系列で十分と言えます。

Lokadのアプローチ

従来型予測（つまり予測）において、精度の概念で仮定される「単純さ」は、ほとんどが過大評価されている、と私たちは考えています。予測、平均、変位は一様に、オーバーフィッティングに左右されがちであり、それは予測モデルの比較を非常に複雑化するものです。しかし、ピンボールロス機能は二つの予測モデルの「相対的｣制度を査定する単純な手法と言えます。

参考文献