概率预测定义
首页 » 知识库 » 此处
作者:Joannès Vermorel,2015 年 10 月
概率预测是指针对某个随机变量未来所有可能出现的结果估算相应的概率。相比单一值预测,例如中位数时序预测或分位数预测,概率预测可以说是一种概率密度函数。概率预测可以应用于诸多领域,例如天气预报、体育博彩等等,但尤其适合用于供应链优化。
应用于供应链优化
从统计角度来说,供应链中的大部分成本源自极端事件。异常高的需求水平会导致缺货,异常低的需求水平会导致库存周转慢,在最极端的情形下甚至会导致库存积压。因此,正确估计此类负面事件的概率对于平衡资源分配(主要是存货的流动资金)与供应链服务质量尤其重要。单一值预测倾向于测重平均数或中位数情形,但此类情形并未正确反映上述极端情况。实际上,问题的重点不在于预测质量(预测结果可能或多或少准确),而在于预测本身的定义:中位数预测不能解决极端事件的问题。传统上在供应链中是通过安全库存分析来解决这个问题的。但是,这种分析通常基于一些强势假设,例如需求呈正态分布,这在供应链中是极其不准确的。
相反,概率需求预测则能够实施优先订货策略,该策略超越了大部分传统订货策略,因为此类策略采用了基于未来需求概率估算的准确结构。
对时序应用概率预测
时序可能是供应链中最常见的数据模型。在本节中,我们要在时序环境中将概率预测概念稍微形式化。假设 $\mathbf{y}_t$ 为时间点 $t$ 的过去需求矢量。我们可以按照如下对每个预测水平线 $h$ 在时间点 $t+h$ 的未来需求建模: $$y_{t+h}=g_h(\mathbf{y}_t)+\epsilon_{t+h}$$ 其中,
- $g_h$ 为水平线 $h$ 特定的预测模型
- $\epsilon_{t+h}$ 表示模型误差
此时,$g_h$ 仍是单一值预测模型。我们可以考虑下面的关系,来将该定义调整为概率预测: $$Y_{t+h}=G_h(\mathbf{y}_t)$$ 其中 $G$ 返回的不会是单一值 $y_{t+h}$,而是具有显式密度分布的随机变量 $Y_{t+h}$,即 $P(y_{t+h}\leq y | \mathbf{y}_t)$。虽然这些内容超出了本章节的范畴,但要注意的一点是,概率预测可以简化为估算累积分布函数。
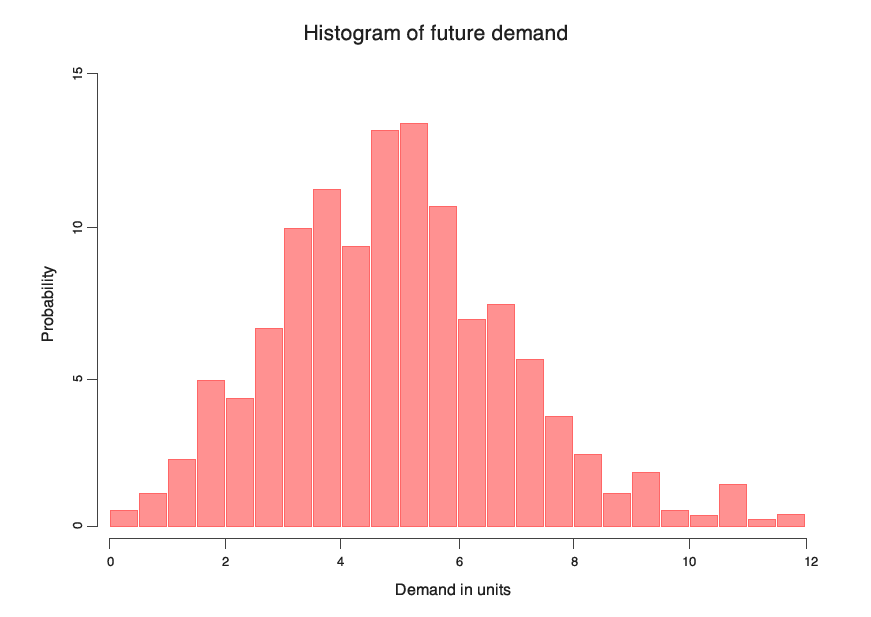
概率预测的实际表示
从实际角度来说,概率预测 $Y_{t+h}$ 通常用直方图表示,其中每个直条表示未来需求的区间,直条高度表示该未来需求落在存储桶相关区间内的预计概率。除非对于该种需求的概率分布可以做出特定的假设,否则在表示需求时直方图会引入一定程度的近似数值。实际上,许多概率分布是无界的,任意大的值也可能存在非零概率。此类分布不能通过有限的直方图来正确呈现。同样,直方图会按结构对每个存储桶内精细的分布结构进行平均。
相比单一值(如非概率预测),直方图在进行处理时需要使用多得多的计算资源,尽管如此,处理大量时序(或更多)的直方图对于现代计算系统不成问题。实际上,直方图可以设计为包含足够多的桶数,以确保需求离散引入的数值不精密之处与预测本身的不确定性相比可以忽略。