Les distributions mathématiques sont puissantes et utiles pour modéliser de nombreuses situations commerciales, notamment lorsque la part d’incertitude est importante. Envision traite comme des VIP les « distributions » sur lesquelles une large gamme d’opérations peut être exécutée. L’ensemble de ces opérations sont désignées sous le terme « algèbre des distributions » pris en charge par Envision. Dans le présent article, nous présentons le type de données des distributions et passons en revue les opérateurs et fonctions qui s’y appliquent.
Le type de données des distributions
Une distribution mathématique est un objet qui
généralise la notion de fonctions. Dans Envision, notre ambition est plus modeste et ce que nous appelons distributions sont en réalité des fonctions $f : \mathbb{Z} \to \mathbb{R}$. Nous appelons ces fonctions (mathématiques) des « distributions » car le cas d’emploi le plus fréquent dans Envision consiste à gérer des « distributions de probabilités », qui sont des distributions strictement positives dont la masse est égale à 1.
Avec Envision, les distributions sont matérialisées via un type de données spécifique appelé « distribution ». Les autres types de données sont notamment « nombre » et « texte ». Le type de données distribution présente des fonctionnements relativement complexes, car il s’agit de fonctions et non de valeurs simples. Par exemple, ci-dessous, nous générons une
distribution de Dirac, une fonction discrète nulle en tout point sauf en 42 où elle vaut 1.
d := dirac(42)
Les distributions peuvent être exportées dans un fichier grâce aux
fichiers de données Ionic. Elles ne peuvent cependant pas être exportées « telles quelles » dans des fichiers CSV et Excel.
Envision offre de nombreuses autres façons de générer des distributions. Nous les passons en revue dans la suite.
Représentation graphique d'une distribution
Les distributions peuvent être représentées à l'aide d'histogrammes. Prenons une simple distribution qui suit la
loi de Poisson :
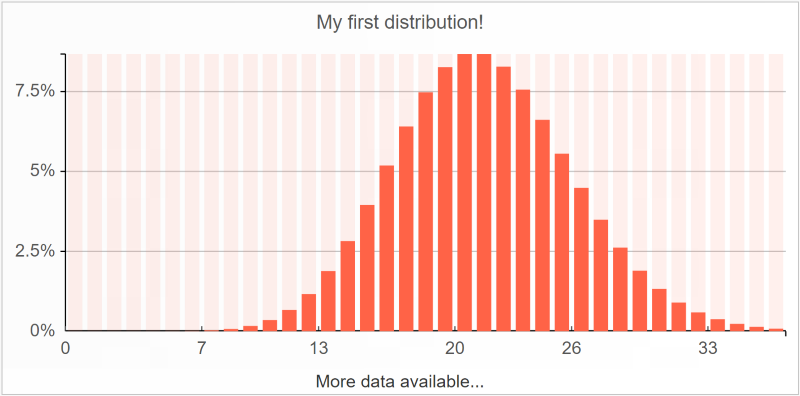
Ce graphique a été généré dans Envision au moyen de l'instruction ci-dessous :
show histogram "My first distribution!" tomato with poisson(21)
La vignette
histogram attend une distribution scalaire simple après le mot clé
with.
Opérations simples
Les opérations les plus simples sur les distributions sont celles qui s’appliquent à tous les points. Par exemple, si $f$ et $g$ représentent deux distributions $\mathbb{Z} \to \mathbb{R}$. Alors l’addition peut être définie comme suit :
$$f+g: k \to f(k) + g(k)$$
Du point de vue d’Envision, si
X et
Y sont des vecteurs de distribution, la même opération s’écrit également :
Z = X + Y
Même lorsque ce sont des distributions qui sont manipulées, Envision reste un langage de vecteurs. Ainsi, nous ne traitons pas une seule distribution à la fois mais l’ensemble du vecteur de distributions. La même opération peut s’effectuer du point de vue scalaire comme suit :
Z := X + Y
Dans cette section et les suivantes, lorsque
X et
Y sont utilisés dans des exemples de script, nous supposons que ces deux variables sont des distributions.
La multiplication et la soustraction sont définies ainsi :
$$f \times g: k \to f(k) \times g(k)$$
$$f-g: k \to f(k)-g(k)$$
Ce qui se traduit de façon très transparente dans la syntaxe Envision suivante :
Z = X * Y
Z = Z - Y
Un nombre $\alpha$ pouvant être implicitement assimilé à une fonction constante $f_{\alpha}: k \to \alpha$, Envision permet de combiner des nombres et des distributions, mais uniquement si la distribution qui en résulte est compacte.
// OK, elle est compacte
Z = 2 * X
/ pas de division par zéro, OK
Z = X / 2
// incorrecte, ce n’est pas une distribution compacte
Z = X + 1
// incorrecte, Y est une distribution compacte et comporte donc des valeurs nulles
Z = X / Y
Les distributions peuvent également être décalées. L'
opérateur de décalage s'écrit généralement comme suit :
$$f_{n}: k \to f(k+n)$$
La syntaxe Envision correspondante est :
Z = X << n // left shift
Z = X >> n // right shift
Naturellement, si
n est négatif, les opérateurs de décalage fonctionnent mais le décalage à gauche devient un décalage à droite et inversement.
Création de distributions
Il existe plusieurs façons de créer des distributions. Le moteur de prévisions de Lokad génère des distributions qui représentent les
délais d'approvisionnement futurs ou la
demande future. Une fois ces distributions sérialisées dans une grille(*), il est possible de générer à nouveau à la distribution grâce à la fonction
distrib(). La syntaxe est la suivante :
Demand = distrib(Id, G.Probability, G.Min, G.Max)
La variable
Demand qui en résulte est une variante. Lorsque la grille d’origine contient des segments dont la longueur est supérieure à 1,
distrib() répartit la masse uniformément sur le segment. La masse de la distribution est conservée par la fonction
distrib().
(*) La sérialisation d’une distribution consiste à transformer ses données dans un format de table classique qui peut être stocké dans un fichier plat. Pour gérer la distribution comme telle, et non comme une table, il faut tout d’abord désérialiser la table. C’est ce que fait la fonction distrib() ci-dessus.
De plus, Envision offre la possibilité de générer une distribution directement à partir d’un ensemble de valeurs numériques constatées. C’est l’objectif de l’agrégateur {ranvar()}} :
X = ranvar(Orders.Quantity)
L’agrégateur {ranvar()}} renvoie une « variable aléatoire » qui correspond à la fréquence observée dans les groupes d’agrégation. Lorsqu’il n’y a rien à agréger,
ranvar() renvoie
dirac(0).
Enfin, il est possible de générer une distribution à partir d'une série temporelle, à l'aide de l'agrégateur
ranvar.segment().
D = ranvar.segment(
// première date pour chaque article
start: Items.Start
// dernière date pour chaque article
end: Items.End
// durée pour chaque article
horizon: Items.Horizon
// entier permettant d'ignorer certains éléments
step: Items.Step
// date de chaque événement
date: Orders.Date
// quantité de chaque événement
quantity: Orders.Quantity)
Pour chaque article, est calculée la distribution de la somme des quantités d'événement pour des périodes d'une durée comprise entièrement entre la première et la dernière date de l'article. En général, la durée correspond au délai d'approvisionnement de l'article.
Transformer une distribution en table
Dans la section précédente, nous avons présenté comment agréger une table en une distribution. L'inverse, transformer une distribution en table, est également possible grâce à la fonction
extend.distrib(). La syntaxe est la suivante :
X = poisson(1)
table G = extend.distrib(X)
G.Probability = int(X, G.Min, G.Max)
show table "My Grid" with
Id
G.Min
G.Max
G.Probability
X est le vecteur de distribution généré à la ligne 1 comme une distribution qui suit la loi de Poisson. À la ligne 2, les distributions sont ajoutées à la table
G. Cette table a une affinité
(Id, *) et, comme illustré aux lignes 3 à 7, contient automatiquement les colonnes numériques
G.Min et
G.Max.
G.Min et
G.Max sont les limites des intervalles comprises dans ces derniers.
Lorsque la distribution est relativement compacte, la table obtenue contient généralement des lignes d'incréments +1 — c'est à dire
G.Min et
G.Max + 1 d'une ligne à l'autre. Cependant, si nous devions transformer des distributions de valeurs élevées,
dirac(1000000) par exemple, il serait inefficace de générer des millions de lignes. Ainsi, la fonction
extend.distrib() agrège les distributions de valeurs élevées en lots plus importants. C'est pourquoi
G.Min et
G.Max sont les limites du lot.
Pour mieux contrôler la granularité des lots générés, la fonction
extend.distrib() offre une première surcharge :
table G = extend.distrib(X, S)
S est un vecteur numérique. La table obtenue contient des lots cohérents avec les segments [0;0] [1;S] [S+1; S+M] [S+M+1;S+2*M] ..., où
M est la taille de lot par défaut — également appelé « multiple ». Cette surcharge est généralement utilisée lorsque doit être prise en compte la demande au-delà du stock total.
Enfin, la deuxième surcharge de
extend.distrib() étend le contrôle avec :
table G = extend.distrib(X, S, M)
M est une taille de lot obligatoire. Si
M est zéro, alors la taille par défaut est utilisée et ajustée automatiquement par Envision. Cette deuxième surcharge est particulièrement utile lorsque des « multiples de lot » entrent en jeu dans le processus de commande et que la demande doit être séparée en lots d'une taille donnée.
Attention, il se peut que
extend.distrib(X, S, M) ne fonctionne pas, selon la capacité allouée à votre compte Lokad, si vous essayez de transformer une distribution de valeurs élevées avec un multiple faible.
Application de produits de convolution sur des distributions
Les
produits de convolution représentent une classe plus avancée d’opérations sur les distributions. Ils sont principalement utilisés lorsque des « variables aléatoires » sont impliquées. À la différences des opérations simples, les produits de convolution ont des interprétations probabilistes telle que la somme ou la multiplication de variables aléatoires indépendantes. Les produits de convolution sont reconnaissable dans Envision grâce à leur opérateurs à deux caractères qui se terminent en ((*)), à savoir :
// produit de convolution additif
Z = X +* Y
// produit de convolution de soustraction, similaire à X +* reflect(Y)
Z = X -* Y
// produit de convolution multiplicatif
Z = X ** Y
// convolution itérée
Z = X ^* Y
Le produit de convolution additif (resp. de soustraction) peut être interprété comme la somme (resp. soustraction) des deux variables aléatoires indépendantes $X+Y$ (resp. $X-Y$). Le produit de convolution multiplicatif, également connu comme la
convolution de Dirichlet, peut être interprété comme le produit de deux variables aléatoires indépendantes.
La convolution itérée est plus complexe. Elle représente ceci :
$$X ^ Y = \sum_{k=0}^{\infty} X^k \mathbf{P}[Y=k] \text{ where } X^k = X + \dots + X \text{ ($n$ times)}$$
Cette dernière opération est intéressante de par sa relation avec le processus qui mène aux
prévisions intégrées de la demande. $X$ représente alors la demande quotidienne —supposée constante — et $Y$ les délais d'approvisionnement probabilistes.
Voir également notre page sur la convolution itérée.
Historique
Le moteur de prévisions de Lokad fournit des « grilles quantiles » depuis début 2015. Ces grilles ne correspondaient pas encore « exactement » des distributions de probabilités — ce n’étaient que des prévisions quantiles interpolées — mais s’en rapprochaient. En travaillant avec nos clients, nous avons pris conscience de l’énorme potentiel de l’analyse probabiliste en matière d’optimisation logistique quantitative. Cependant, nos « grilles » ne restaient que de grosses tables qui listaient toutes les probabilités. Elle ont pourtant représenté une avancée pour nos clients et nous-même : nous avons rapidement réalisé que le traitement de probabilités sous forme de listes n’est pas aisé.
L'« algèbre des distributions » est une réponse technologique proposée par Lokad aux difficultés rencontrées en logistique face à l'incertitude des futurs. En effet, ces difficultés ne peuvent être résolues avec une seule prévision médiane, elles requièrent une analyse complète de tous les risques associés à chaque possibilité. Envision fait sienne l'idée que « tous les scénarios » doivent être pris en compte et pas seulement quelques-uns. Pour cela, des variables aléatoires peuvent être utilisées dans les scripts Envision et manipulés via des opérations conçues spécifiquement, telles que les « convolutions » détaillées plus bas. En pratique, l'algèbre des distributions est un moyen élégant de modéliser des situations logistiques complexes dans lesquelles la demande et les délais d'approvisionnement futures sont incertains.
