Estacionalidad (cadena de suministro)

Por Joannès Vermorel, última revisión: septiembre de 2011

En la cadena de suminsitro, se dice que la demanda —o las ventas— de un determinado producto muestra estacionalidad cuando la serie de tiempo subyacente atraviesa una variación cíclica predecible, dependiendo de la época del año. La estacionalidad es uno de los patrones estadísticos más utilizados para mejorar la precisión de los pronósticos de demanda.

Ilustración de series de tiempo estacionales

El gráfico a continuación ilustra 4 series de tiempo estacionales (haga clic para agrandar). Las series de tiempo son agregadas a nivel semanal durante un período de 159 semanas (alrededor de 3 años). Los datos representan los envíos semanales correspondientes a 4 productos distintos del depósito de un gran minorista europeo.



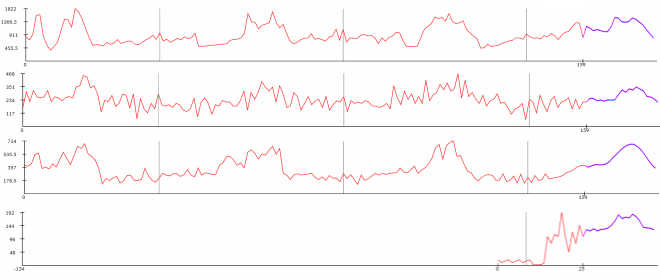
El primer día del año (1.º de enero) está señalado con un marcador vertical gris. Los datos históricos aparecen en rojo, mientras que el pronóstico de Lokad se muestra en color violeta. La estacionalidad se puede observar como una similitud de patrones de un año a otro. Utilice los marcadores grises como referencia.

Modelo básico para la descomposición estacional

La Y(t) corresponde a la demanda en el momento t. Descomponemos la demanda Y(t) en dos componentes: S(t), una función estrictamente cíclica, y Z(t), el complemento no estacional. Esto da:

Y(t) = S(t) * Z(t) donde S(t + 1 año) = S(t)

Si la función S(t) puede ser calculada, entonces el proceso de pronóstico generalmente pasa por tres etapas:

1. Calcular las series de tiempo desestacionadas como Z(t) = Y(t) / S(t).
2. Elaborar el pronóstico a partir de las series de tiempo Z(t), en lo posible mediante la media móvil.
3. Volver a aplicar los índices de estacionalidad a los pronósticos.
   

Volviendo al problema inicial de calcular los índices estacionales S(t), suponiendo que no existe una tendencia (entre otros) S(t) puede ser calculada con:

S(t) = AVERAGE( Y(t-1)/MA(t-1) + Y(t-2)/MA(t-2) + Y(t-3)/MA(t-3) + ... )

donde Y(t-1) es la abreviación para Y(t - 1 año) y MA(t) la media móvil en 1 año de Y(t).

El método propuesto en esta sección es un poco ingenuo, pero puede ser implementado fácilmente en Excel. En la literatura específica se pueden encontrar muchos modelos para abordar la estacionalidad con métodos más complicados. Por ejemplo: Box-Jenkins, ARMA, ARIMA, Holt-Winters...

Desafíos en el cálculo de índices de estacionalidad

El modelo de estacionalidad ilustrado más arriba es un abordaje un tanto ingenuo que puede funcionar para las series de tiempo estacionales llanas. Sin embargo, hay varias dificultades prácticas que se presentan al calcular la estacionalidad:

1. Las series de tiempo son cortas. La vida útil de muchos bienes de consumo no excede los 3 o 4 años. Como resultado, para un determinado producto, la historia de ventas ofrece, en promedio, muy pocos puntos en el pasado para calcular cada índice estacional (es decir, los valores de S(t) durante el curso del año. Ver sección precedente).
2. Las series de tiempo presentan ruido. Las fluctuaciones arbitrarias del mercado tienen impacto sobre las ventas, y hacen difícil aislar la estacionalidad.
3. Varias estacionalidades involucradas. Cuando se observan las ventas a nivel de tienda, la estacionalidad del producto en sí generalmente está entrelazada con la estacionalidad de la tienda.
4. Otros patrones, como la tendencia o el ciclo de vida del producto, también tienen impacto en las series de tiempo, introduciendo varios tipos de desviaciones en el cálculo.
   

Un método simple —aunque requiere de mucho personal— para abordar estos problemas consiste en crear en forma manual perfiles de estacionalidad a partir de agregados de productos de los que se sabe que tienen igual comportamiento estacional. La vida útil del agregado de producto es generalmente más larga que la vida útil de los productos individuales, lo que elimina esos problemas de cálculo.

Cuasi-estacionalidad

Hay muchos patrones que se presentan una vez al año, pero no siempre en la misma fecha’. En Lokad, los llamamos patrones cuasi-estacionales. Por ejemplo, el Día de la Madre (que cae en fechas diferentes dependiendo del año y también varía según el país) y otras festividades, como el Ramadán, la Pascua y el Janucá (que caen en fechas diferentes según el año), son cuasi-estacionales.

Esos eventos cuasi-estacionales exceden el alcance de los modelos clásicos de pronóstico cíclico que suponen que el período del ciclo es siempre constante. Para abordar esos eventos cuasi-estacionales, se requiere una lógica cuasi-cíclica más compleja.