分布代数
首页 » 资源 » 此处
在对多种商业情形,尤其是存在不确定性的商业情形建模时,可以利用数学分布这种强大而实用的途径。Envision 将分布视为“一等公民”,且可以处理要对这些分布执行的各种运算。所有这些运算统称为分布代数,并且 Envision 支持这些分布代数。在本页面,我们将介绍分布数据类型,并了解各种相关的运算符和函数。
前言
Lokad 预测引擎于 2015 年初开始提供分位数网格。严格来说这些网格并非现在的概率分布——只不过是经过内插的分位数预测而已,但当时已经非常接近了。在与客户合作的过程中,我们开始意识到对定量供应链优化应用概率分析的巨大潜力。但是,我们的网格只是罗列所有概率的大型表格而已。无论是对于我们的客户还是我们自身,这些网格都意味着一种突破,我们很快认识到用列表的形式表示处理概率并非易事。分布代数是 Lokad 针对未知的未来所存在的供应链挑战而做出的广泛技术解答。实际上,这些情形并不只是需要单一的中位数预测,而是需要针对所有可能性进行全面的风险分析。Envision 所持的是所有情形都应当予以考虑的观点,而不只是侧重于为数不多的情形。为此,可以在 Envision 脚本中引入随机变量,并通过专门为随机变量量身定制的运算(例如卷积)加以处理,详情参见下文。分布代数是对未来需求以及未来交付周期皆不确定的复杂供应链情形建模的良好方式。
分布数据类型
所谓数学分布,是指广义化函数概念的对象。在 Envision 中,我们的目标是构建更加适中的分布,实际上我们称之为函数 $f: \mathbb{Z} \to \mathbb{R}$。之所以称这些(数学)函数为分布,是因为 Envision 中最常见的使用情况就是处理概率分布,即质量等于 1 的严格正态分布。此外,Envision 分布(下文简称“分布”)很紧凑:它们只允许有限数量的值非零。之所以引入这种约束,是因为非紧凑的分布可能会生成众多实际意义甚微的复杂情形。
Envision 中的分布是通过一种叫做分布的数据类型实现分布的,而不是通过数值或文本等其他数据类型。分布数据类型之所以能准确表现出相对复杂的行为,是因为它是一个函数,而不是单一的值。举个例子,下文我们将生成一个狄拉克函数,狄拉克函数是一种离散函数,在除点 42 以外的其他点的值都为 0,而点 42 的值为 1。
d := dirac(42)
通过 Ionic 数据文件可以将分布导出到文件中,但不能像这样将分布导出到 CSV 或 Excel 文件中。 Envision 提供了多种生成分布的方式。下文将对此进行介绍。
对分布绘图
分布可以通过直方图实现可视化。来看一个简单的泊松分布: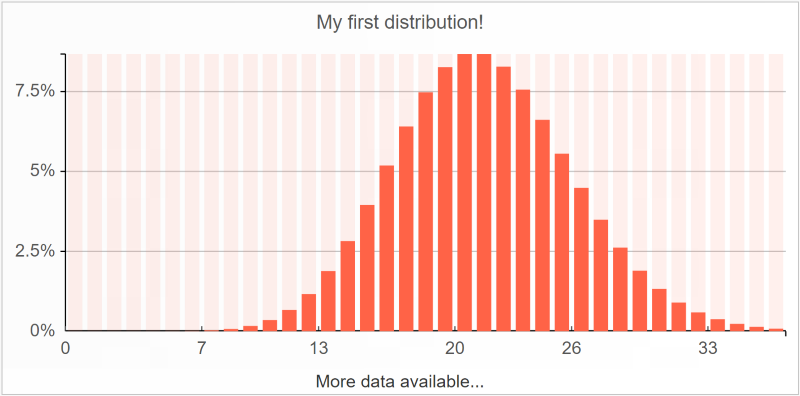
此图在 Envision 中由单独一行生成,详情如下:
show histogram "My first distribution!" a1d4 tomato with poisson(21)
histogram 磁贴预期的是在 with 关键字后面提供单一标量分布。点态运算
最简单的分布运算就是点态运算。举个例子,令 $f$ 和 $g$ 表示两种分布 $\mathbb{Z} \to \mathbb{R}$。那么,相加可以定义为:$$f+g: k \to f(k) + g(k)$$
从 Envision 的角度来看,假设
X 和 Y 都是分布向量,同样的运算也可以写成:
Z = X + Y必须注意,即便是在处理分布时,Envision 仍是一种向量语言。因此,我们通常不一次处理一种分布,而是同时处理整个分布向量。使用下面的公式可以对标量执行同样的运算:
Z := X + Y在本节以及下面的章节中,只要是脚本示例中用到
X 和 Y,都假定这两个变量为实际分布。 所以,点态相乘和相减可以定义为: $$f \times g: k \to f(k) \times g(k)$$ $$f-g: k \to f(k)-g(k)$$ 它们可以相当透明地转化为下列 Envision 语法:
Z = X * Y Z = Z - Y当数值 $\alpha$ 可以隐式同化为常数函数 $f_{\alpha}: k \to \alpha$ 时,Envision 允许组合数值与分布——但前提是得到的分布为紧凑型分布。
Z = 2 * X // OK, it's compact Z = X / 2 // not dividing by zero is OK Z = X + 1 // incorrect, not a compact distribution Z = X / Y // incorrect, Y is compact hence has zero values分布也可以移位。移位运算符通常这样书写:
$$f_{n}: k \to f(k+n)$$ 相应的 Envision 语法为:
Z = X << n // left shift Z = X >> n // right shift当然,如果
n 为负数,移位运算符将正常工作,但左移位变为右移位,而右移位变为左移位。生成分布
创建分布的途径很多。Lokad 预测引擎针对未来的交付周期或未来的需求生成分布。当这些分布序列化为网格 (*) 时,即可通过distrib() 函数重新生成分布。相关语法如下:
Demand = distrib(Id, Grid.Probability, Grid.Min, Grid.Max)得到的
Demand 变量即为分布。当原始网格包含比 1 长的段时,distrib() 会在此段均匀分布质量。分布质量由 distrib() 函数保存。 (*) 分布序列化,即分布数据转化成可以作为平面文件保存的常规表格格式的过程。要想将分布作为实际分布处理,而不是作为表处理,需要先对此表进行反序列化。这正是
distrib() 函数的功能。此外,Envision 还提供了直接从一组观测到的数值生成分布的功能。这就是
ranvar() 聚合器的作用所在:
X = ranvar(Orders.Quantity)
ranvar() 聚合器返回与聚合组中观测到的频率相匹配的随机变量。当没有可供聚合的对象时,ranvar() 返回 dirac(0)。将分布延展到表中
在上一节中,我们了解了表如何聚合成分布。我们也可以执行逆向过程——将分布延展到表的行中。在这一节,我们将了解用于执行此功能的extend.distrib() 函数。语法如下:
X = poisson(1) table Grid = extend.distrib(X) show table "My Grid" with Id, Grid.Min, Grid.Max, Grid.Probability其中
X 为第 1 行作为泊松分布生成的分布向量。在第 2 行,分布延展到一个叫做 Grid 的表中。此表具有 (Id, *) 相关性。在第 3 行,表中自动填充数值列 Grid.Min、Grid.Max 和 Grid.Probability。Grid.Min 和 Grid.Max 均包括边界在内。在延展相对紧凑的分布时,得到的表通常包含以 +1 为增量的行,也即
Grid.Min 和 Grid.Max 以 +1 为增量从一行延伸到下一行。但是,如果考虑的是高值分布,例如 dirac(1000000),那么生成数百万行的效率极低。因此,函数 extend.distrib() 将把大型分布聚合成厚度更大的桶。这就解释了为什么我们使用 Grid.Min 和 Grid.Max 来表示桶的边界(边界也包括在内)。为了对所生成的桶的粒度进行进一步控制,函数
extend.distrib() 将提供第一个过载:
table Grid = extend.distrib(X, S)其中
S 为数值向量。得到的表提供了与 [0;0] [1;S] [S+1; S+M] [S+M+1;S+2*M] ... 等段进行了统合的桶,其中 M 为默认的桶大小,也称为倍数。此过载通常出现在需要考虑需求超出总库存的时候。最后,
extend.distrib() 的第二个过载提供了更进一步的控制:
table Grid = extend.distrib(X, S, M)其中
M 为强制的桶大小。如果 M 为 0,延展将恢复为默认的桶大小,并由 Envision 自动调整。第二个过载对于订货过程涉及到批次倍数的情形尤其有用,因为此需求需要成批纳入特定大小的桶中。请注意,如果尝试以低倍数延展高值分布,
extend.distrib(X, S, M) 可能会失效,具体取决于为您的 Lokad 帐户分配的容量。参数分布
Envision 也提供了多种参数分布,也即以数值作为参数的函数,此类函数返回的是分布。dirac(n)返回除n以外所有位置的值为 0 而n位置的值为 1 的函数。identity(n)返回函数 $\text{id}: k \to k$,但仅限于段 [0;n],其他位置返回 0。uniform(n)返回函数 $\text{unif}: k \to 1$,但仅限于段 [0;n],其他位置返回 0。uniform(m, n)返回函数 $\text{unif}: k \to 1$,但仅限于段 [m;n],其他位置返回 0。uniform(D)返回函数 $\text{unif}: k \to 1$,但仅限于分布D的正值,其他位置返回 0。poisson(a)返回参数a(在文献资料中为 $\lambda$)的泊松分布。exponential(a)返回参数a(在文献资料中为 $\lambda$)的指数分布。
与分布有关的函数
从分布中也可以获取数值指标。crps(X, A),其中A为整数,返回连续概率排位分数 (CRPS)。mean(X)返回统计平均值。variance(X)返回统计方差。mass(X)返回分布质量,也即 $\int_{-\infty}^{\infty}f(k) dk$isranvar(X)返回布尔值。当分布为随机变量时,返回true。int(X, A, B),当A和B为整数时,返回X对相容段 [A;B] 的积分。quantile(X,tau)返回分布的分位数;例如最小 $x$,$\mathbf{P}[X \leq x] \geq \tau$。spark(X)返回文本值,此值包含分布的紧凑型 ascii-art 表示。
分布转化
一种分布可以转化为另一种分布。reflect(X)返回反射分布 $k \to f(-k)$。transform(X,a)返回通过内插 $k \to f(k / a)$ 求近似值的分布。fillrate(X)返回边际供货率。其输入应为随机变量,且返回随机变量。truncate(X, A, B)返回截断后的分布 $k \to f(k) \text{ if } x \in [a;b] \text{ else } 0$。界限A和B包含在内。
概率分布的卷积运算
卷积是对分布进行的一类更加高级的运算。卷积的主要使用场合涉及随机变量。与点态运算不同,卷积具有概率解译,例如加上或乘以独立的随机变量。在 Envision 中,卷积通过末尾为* 的双字符运算符进行识别,也即:
Z = X +* Y // 加卷积 Z = X -* Y // 减卷积,与 X +* reflect(Y) 相同 Z = X ** Y // 乘卷积 Z = X ^* Y // 卷积幂加卷积(与之相对的是减卷积)可以解译为对两个独立的随机变量 $X+Y$(与之相对的是 $X-Y$)相加(与之相对是相减)。乘卷积也称为 Dirichlet 卷积,可以解译为两个独立随机变量的乘积。
卷积幂较为复杂,可以表示为: $$X ^ Y = \sum_{k=0}^{\infty} X^k \mathbf{P}[Y=k] \text{ where } X^k = X + \dots + X \text{ ($k$ times)}$$ 最后这项运算很有趣,因为它与得出完整需求预测的过程息息相关,其中 $X$ 表示每日需求(假设是不变的),$Y$ 表示交付周期概率。
另请参阅卷积幂页面。