Par Gaël Grasset, Juillet 2015La détermination de prix magiques est une méthode de tarification qui vise à maximiser les bénéfices en effectuant de petits ajustements sur la structure des prix. Cette méthode repose sur l'hypothèse que les consommateurs n'aiment pas faire des calculs et lisent donc uniquement les premiers chiffres d'un prix au moment de leurs achats. Ainsi, ils tirent leurs informations principalement des premiers chiffres du prix plutôt que des derniers, en d'autres termes c'est l'ordre de grandeur qui leur importe. Par exemple, le prix 17,99 € semble plus proche de 17 € que de 18 €.
Cette méthode de tarification est largement répandue. D'après Judith Holdershaw et coll., plus de 90 % des prix en Nouvelle Zélande finissent par un chiffre supérieur à 5 et 60 % par un « 9 ».
Pourquoi utiliser des prix magiques ?
Cette stratégie repose sur le fait que les consommateurs attachent une grande importance au temps passé à évaluer les prix. Ce dernier augmentant avec le nombre de chiffres, les premiers chiffres sont plus importants que les derniers. Il est donc possible de définir un taux d'importance pour chaque chiffre et d'en déduire les concepts de « prix perçu » et de « prix réel ».
« Un consommateur doit évaluer le prix 1743,99 €. Le premier chiffre représente plus de 50 % de l'information car 1000 € représentent plus de 50 % du prix, le consommateur va donc lire et comprendre clairement cette valeur. Le deuxième chiffre (700 €) représentant près de 40 % de la signification du prix, le consommateur lit également cette valeur. Puis, le troisième chiffre (40 €) n'apporte que 2 % de l'information sur le prix, il est donc moins important. Dans ce cas, le prix important pour le consommateur est 1740,00 € ou 1700,00 €, selon le niveau d'importance souhaité. »
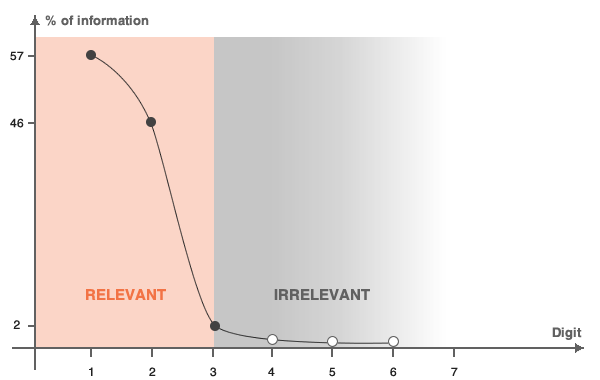
Une fois la partie « importante » du prix définie, c'est à dire la partir « perçue », la maximisation de la marge peut intervenir en transformant les chiffres de moindre importance en des « neufs ». L'ajout de chiffres de « moindre importance » ne modifie pas le prix perçu et n'a donc aucune conséquence sur la demande ou sur les ventes d'un article en particulier. Les chiffres supplémentaires — non perçus — du prix entrent entièrement dans les bénéfices. C'est le cas des 99 centimes de l'exemple ci-dessus. Étant donné le prix total du produit, les 99 centimes n'impactent pas la décision des consommateurs d'acheter le produit et entrent donc entièrement dans les bénéfices.
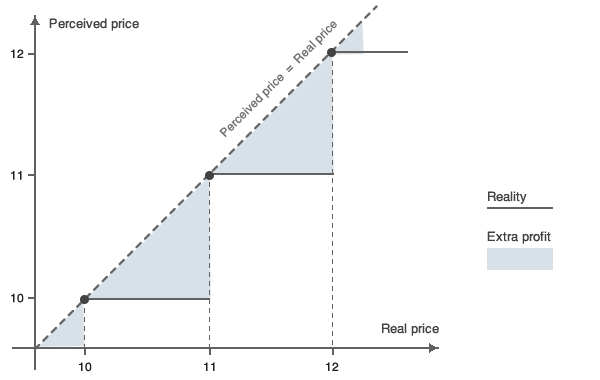
Les plages de prix doivent être prises en compte lors de l'application de cette méthode. En effet, aujourd'hui la plupart des sites Web de commerce électronique offrent la possibilité de filtrer les articles par plage de prix, comme 50-99 € par exemple, et un article dont le prix est 99,99 € (et non 100 €) passe le filtre de cette plage, ce qui peut avoir un impact positif sur la demande.
Cette méthode a également deux effets positifs dans le domaine de la comptabilité. Tout d'abord, si tous les prix finissent par « ,99 », il est facile de calculer le montant quotidien des ventes. Par exemple, si la trésorerie à la fin de la journée finit par « ,38 », 62 (ou 162, 262, etc.) ventes ont eu lieu ce jour-là. De plus, cette méthode de tarification complique les vols dans la caisse dans les entreprises où le personnel y a accès facilement (dans les supermarchés par exemple). Il faudrait en effet que le voleur prenne une somme qui comprenne un multiple de « ,99 » pour que son méfait passe inaperçu, ce qui est plus difficile qu'avec des prix ronds.
Est-ce que ça fonctionne ?
La demande évolue-t-elle entre des prix en « ,99 » et en « ,00 » ? Si oui, cela signifie que le signal envoyé par des prix en « ,99 » est plus fort que le 1 % qui sépare les deux types de prix.
D'après Guéden et coll., cet effet peut être très significatif. Leur étude portait sur un petit restaurant pizzeria-grill en France. Une liste de neuf plats principaux était proposée dans le restaurant et comprenais cinq pizzas. L'effet de la modification de la fin du prix d'une pizza était testé. Pendant 2 semaines, toutes les pizzas étaient proposées avec un prix rond en « ,00 » (9,00 € par exemple) tandis que pendant 2 autres semaines une pizza cible était proposée à un prix en « ,99 » (8,99 € par exemple) et les autres toujours à un prix rond en « ,00 ». Enfin, pendant une troisième période de 2 semaines, toutes les pizzas étaient proposées à un prix en « ,99 ».Les résultats ont montré une augmentation de la demande pour la pizza cible lorsque celle-ci était à un prix en « ,99 » et que les autres étaient à un prix rond en « ,00 ». Aucune différence n'a été constatée lorsque tous les prix finissaient de la même façon (en « ,00 » ou en « ,99 »). Ainsi, l'effet d'un prix en « ,99 » en comparaison à des prix ronds peut être très positif pour les parts de marché.
Schindler et Kibarian ont également étudié les effets des prix magiques mais à plus grande échelle. Ils se sont penchés sur les prix d'un commerce électronique de mode féminine et ont comparé les effets sur les ventes de prix en « ,88 », en « ,99 » et en « ,00 ». Les ventes des articles avec un prix en « ,99 » se sont avérées 8 % plus importantes que celles des articles avec un prix en « ,00 ». Ce ne fut cependant pas le cas des prix en « ,88 ». Selon la théorie des prix magiques, la perception de prix en « ,88 » et en « ,99 » ne devrait pas être différente et ces prix devraient entraîner le même niveau de demande. Les constatations empiriques démontrent pourtant que les prix en « ,99 » déclenchent plus de ventes. Il semble que ce qui importe en matière de prix magiques c'est que le consommateur ait « l'impression » que les produits sont à un « bon prix », impression qui les pousse à acheter.
Quels sont les inconvénients principaux des prix magiques ?
Cette méthode repose sur l'hypothèse que les consommateurs ont tendance à considérer la valeur nominale des prix sans chercher à « comprendre » ce qui se cache derrière leurs derniers chiffres. Mais cette hypothèse ne tient pas toujours. Prenons l'exemple du secteur immobilier. Si l'on s'en tient à l'hypothèse énoncée précédemment, un consommateur ne devrait pas faire de grande différence entre un bien à 1 860 000,99 € et à 1 810 000,99 €. Néanmoins la différence de 50 000 € entre les deux prix est importante et il est peu probable qu'un acheteur ne la prenne pas en compte. Par conséquent, cet exemple montre que les prix magiques ne fonctionnent pas en toute circonstance.
Il existe un autre inconvénient relatif à l'effet psychologique des prix magiques. Les articles dont le prix finit en « ,99 » sont souvent perçus comme promotionnels ou bas de gamme. Il est donc probable que la modification du dernier chiffre d'un prix ait un impact sur la perception de la qualité du produit. Si la qualité estimée d'un produit influe sur la demande, alors les prix en « ,99 » peuvent conduire à une demande moins forte et donc des bénéfices moins importants, puisqu'ils sont associés à une qualité moindre.
« Les consommateurs peuvent considérer qu'une machine à café à moins de 20 € n'est pas assez chère et voir le prix comme un signe de mauvaise qualité. Par conséquent, en fixant le prix d'une machine à café à 19,99 €, la demande peut baisser considérablement. Cet exemple montre l'inefficacité des prix magiques dans ce cas précis. »
Références principales
- Anderson E. T. & Simester D. I., “Price cues and customer price knowledge”, 2008
- Guéguen N., Jacob C., Legoherel P. & Ngobo P., “Nine-ending priceing and consumer’s behavior : A field study in a restaurant”, International Journal of Hospitality Management, 2009
- Holdershaw J., Gendall P. & Garland R., “The widespread of use of odd pricing in the retail sector”, Marketing Bulletin, 1997
- Nyström H., Retail Pricing. An Integrated Economic and Psychological Approach, 1970
- Schindler R. M. & Kirbarian T. M., “Increased consumer sales response though use of 99-Ending prices”, Journal of Retailing, 1996

