LokadTV
Blog
Comics
Contact
Login
Es
English Français Deutsch Español Italiano Русский 中文

Régression quantile

Notebook-as-a-book illustration







Par Joannès Vermorel, février 2012

La régression quantile est un type de régression (c'est-à-dire de prévision) qui introduit volontairement un biais dans le résultat. Au lieu de rechercher la moyenne de la variable à prévoir, une régression quantile cherche la médiane, ainsi que tous les autres quantiles (parfois appelés centiles ou percentiles). Les quantiles sont particulièrement utiles pour l’optimisation des stocks comme méthode directe pour calculer le point de commande.

Régression est ici synonyme de prévision. Le terme de "régression" met l'accent sur l’approche mathématique, tandis que celui de "prévision" met en avant l’utilisation pratique du résultat.

La notion de régression quantile est un sujet statistique relativement avancé. L’objectif de cet article n’est pas de traiter rigoureusement ce sujet, mais plutôt d'en donner une présentation (relativement) intuitive à l'usage des distributeurs ou des fabricants.

Illustration visuelle des quantiles

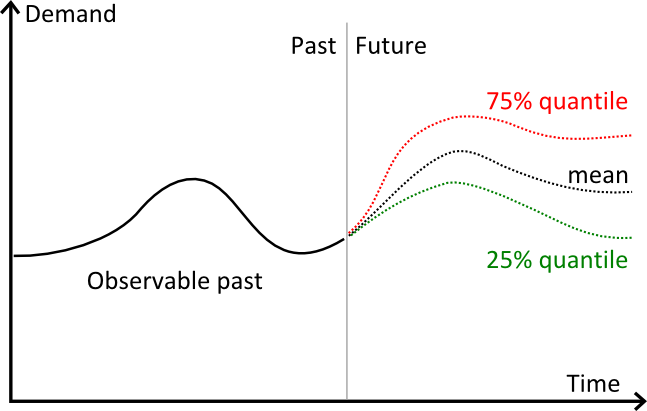
Les séries temporelles des quantiles inférieurs et supérieurs côte à côte avec la série temporelle de la prévision moyenne.

Le graphique ci-dessus illustre 3 prévisions distinctes :
  • en rouge, des prévisions quantiles à 75%.
  • en noir, une prévision moyenne.
  • en vert, des prévisions quantiles à 25%.

Visuellement, les quantiles se comportent quasiment comme des intervalles de confiance. Cependant, en pratique, le quantile est uniquement requis pour un seul pourcentage cible.

Quantiles (ou centiles) de la demande future

La prévision classique, et la plus intuitive, est la prévision moyenne : les poids respectifs de la sur-prévision et de la sous-prévision doivent être égaux, sinon la prévision est biaisée (pour être plus précis, elle est biaisée par rapport à la moyenne).

Même si le fait d'avoir une prévision non biaisée est une propriété souhaitable, cela ne présage en rien de la précision de la prévision. En particulier, une prévision peut être à la fois non biaisée et très imprécise. Le biais renvoie uniquement à la tendance du modèle de prévision à sur-estimer ou sous-estimer le futur.

Une première façon d'affiner cette vision est la prévision médiane : les fréquences respectives de la sur-prévision et de la sous-prévision doivent être égales, sinon les prévisions sont biaisées par rapport à la médiane.

À ce stade, nous avons déjà transformé la notion de prévisions non biaisées en passant de poids égaux à probabilités égales. Ce changement est subtil, mais dans certaines situations, il peut avoir un gros impact numérique.

Illustration : revenu des ménages moyen versus revenu médian aux US

Le revenu des ménages aux US illustre bien la grande différence entre moyenne et médiane.

Selon l’US Census Bureau, en 2004, le revenu médian des ménages était de 44 389 $, tandis que la même année le revenu moyen était de 60 528 $, soit presque 40% de plus que la médiane.

Cet écart s’explique par les revenus élevés (comparativement) des foyers américains les plus riches, comparés au reste de la population. On retrouvera un écart de ce type entre la moyenne et la médiane dans toutes les distributions non symétriques, typiquement toutes les distributions ne suivant pas une distribution normale.

Généralisation de la médiane

La médiane représente le seuil au niveau duquel la distribution est divisée en probabilités de 50/50. Cependant, il est possible de considérer d’ autres rapports de fréquence. Par exemple, on peut choisir 80/20, ou 90/10, ou tout autre rapport ayant un total de 100%.

Les quantiles représentent une généralisation de la médiane à un pourcentage donné. Pour τ, une valeur entre 0 et 1, la régression quantile Q(τ) représente le seuil où la probabilité d’observer une valeur inférieure au seuil est exactement de τ.

Prévisions quantiles

Les prévisions classiques et quantiles prennent toutes deux en entrée des séries temporelles. Les séries temporelles représentent les données en entrée. En plus de ces données, les prévisions moyennes de séries temporelles nécessitent deux paramètres structurels supplémentaires :

  • la période (jour, semaine ou mois).
  • l’ horizon, qui est un nombre entier représentant le nombre de périodes à prévoir.

Implicitement, les séries temporelles sont agrégées selon la période, et l’horizon est choisi suffisamment large pour être utilisé de manière pratique, c'est-à-dire en étant généralement supérieur au délai de réapprovisionnement.

Les prévisions moyennes bénéficient d’une propriété très utile : il est mathématiquement correct de faire la somme des prévisions. Par exemple, si y1, y2, y3 et y4 représentent une prévision sur 4 semaines en avant, alors, si nous avons uniquement besoin de la demande attendue sur les deux prochaines semaines, on peut additioner y1+y2.

Cependant, faire la somme des prévisions quantiles est mathématiquement incorrect, ou plus précisément, la somme des quantiles ne donne pas le quantile de la somme (la somme des segments).

Montrons pourquoi le quantile ne peut pas être additionné. Supposons qu'un joueur joue une pièce d'1 $ aux machines à sous chaque semaine. Supposons que les chances de gagner sont d’1% pour un gain de 50 $ ou de zéro sinon. Si nous examinons le quantile 99% de la récompense attendue, nous obtenons une récompense hebdomadaire de 50 $ pour chaque semaine. Cependant, si nous examinons le quantile 99% sur deux semaines, la récompense attendue est toujours égale à 50 $. En effet, la probabilité de gagner deux fois est seulement de 0,01% (1% multiplié par 1%) ; par conséquent, le quantile 99% reste inchangé. La somme des deux quantiles 99% hebodmadaires donnerait 100 $, mais en réalité, il faut 16 semaines pour accumuler 100 $ de gains pour le quantile 99% (la preuve de ce résultat numérique n’est pas donnée ici, car elle dépasse le cadre de cet article).

Étant donné qu'on ne peut faire la somme des prévisions quantiles, les prévisions quantiles de séries temporelles doivent reconsidérer la notion même d'agrégation par période. En effet, la production de prévisions quantiles par période est discutable, parce que ces prévisions élémentaires ne peuvent pas être combinées pour produire des quantiles corrects sur les segments.

Ainsi, la prévision quantile de séries temporelles vient avec une structure distincte :

  • avec τ le quantile cible, en pourcentage.
  • et λ l’ horizon exprimant une durée (typiquement en jours).

Par exemple, si la série temporelle représente les ventes d’un produit A, et que nous avons τ=0,90 et λ=14 jours, alors la prévision quantile (τ, λ) retournera une valeur de la demande ayant exactement 90% de chance d’être supérieure à la demande totale observée pendant 14 jours (et respectivement 10% de chance d’être inférieure à la demande sur ces mêmes 14 jours).

Contrairement aux prévisions classiques, les prévisions quantiles produisent une et une seule valeur par série temporelle, indépendamment de l’horizon. Dans une certaine mesure, les prévisions quantiles sont plus agnostiques en termes de période que leurs homologues classiques.

L'approche de Lokad

Au premier abord, les prévisions quantiles semblent un peu plus compliquées que les prévisions classiques. Néanmoins, dans de nombreuses situations réelles, les professionnels finissent par produire d'abord des prévisions moyennes, avant de les extrapoler immédiatement en prévisions quantiles, généralement en faisant l'hypothèse que les prévisions suivent une distribution normale. Toutefois, l’étape d'extrapolation représente souvent le maillon le plus fragile du processus, et peut dégrader considérablement le résultat final. La technologie de prévision doit s’adapter aux exigences pratiques, en fournissant des prévisions quantiles natives.

Pour en savoir plus