von Joannès Vermorel, Februar 2012Die Pinball-Loss-Funktion, auch als quantil loss bekannt, ist eine Kennzahl, die zur Beurteilung der Genauigkeit einer Quantilprognose eingesetzt wird.
Die Bewertung der
Genauigkeit einer
Quantil-Prognose ist eine komplexe Angelegenheit. Im Gegenteil zu klassichen Prognosen, deren Ziel eine absolute Nähe zu den beobachteten Werte ist, ist die Situation (absichtlich)
voreingenommen, wenn Quantil-Prognosen betroffen sind. Von daher ist der naive Vergleich
beobachtet vs.
Prognosen nicht zufriedenstellend. Die
Pinball-Loss-Funktion liefert einen Wert, der als
Genauigkeit eines Quantil-Prognose-Modells bezeichnet werden kann.
Formel
Angenommen $\tau$ ist das Ziel-Quanitl, $y$ der Istwert und $z$ die Quantil-Prognose, lautet $L_\tau$, die Pinball-Loss-Funktion, folgendermaßen:
$$
\begin{eqnarray}
L_{\tau}(y,z) & = & (y - z) \tau & \textrm{ if } y \geq z \\\
& = & (z - y) (1 - \tau) & \textrm{ if } z > y
\end{eqnarray}
$$
Pinball-Loss-Funktion.xlsx herunterladen.Anhand der Tabelle ist zu sehen, wie die Pinball-Loss-Funktion innerhalb Microsoft Excel berechnet werden kann. Die eigentliche Formel ist nicht komplizierter als die meisten Präzisionsindikatoren, sowie MAPE.
Illustration
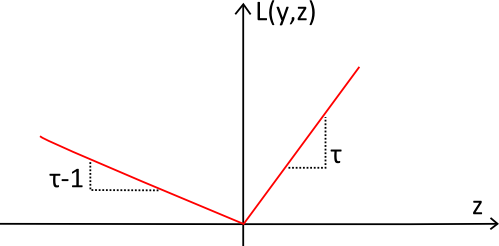
Die Pinball-Loss-Funktion (rot) wurde nach ihrer Form benannt, da diese an die Flugbahn eines Balls in einem
Flipperautomaten erinnert. Die Funktion ist stets positiv und je weiter sie vom Ziel $y$ entfernt ist, desto größer ist der Wert von $L_\tau(y,z)$. Der
Anstieg spiegelt das
gewünschte Ungleichgewicht der Quantil-Prognose wider.
Das beste Quantilmodell hat den niedrigsten Pinball-Loss
Der wichtigste mit der Pinball-Loss-Funktion assoziierte Fakt ist:
Je niedriger der Pinball-Loss, desto genauer die Quantil-Prognose.
Es ist nachweisbar, dass die Funktion, die den Pinball-Loss reduziert, gleichzeitig die optimale Quantil-Prognose liefert. Der für einen Beweis benötigte Formalismus übersteigt jedoch den Rahmen dieses Artikels.
Um die zugehörige Genauigkeit der beiden Quantil-Modelle (z. B. Lokad vs. Konkurrenz) zu vergleichen, muss der
durchschnittliche Pinball-Loss beider Modelle über diverse ausreichend große Zeitreihen berechnet werden, um eine statistische Signifkanz des beobachteten Unterschieds zu gewährleisten. In der Praxis reichen wenige hunderte von Zeitreihen aus, um festzustellen, welches Quantil-Modell
genauere Ergebnisse liefert.
Lokad hat die Lösung
Die angebliche
Einfachheit des Begriffs Genauigkeit in einer klassischen Prognose (d. h. Durchschnittsprognose) ist unserer Meinung nach absolut überbewertet. Prognosen, ob Durchschnitts- oder Quantil-, unterliegen dem
Overfitting, wodurch der Vergleich von Prognosenmodellen erheblich erschwert wird. Die Pinball-Loss-Funktion jedoch bietet eine einfache Art und Weise zur Bewertung der
relativen Genauigkeit von zwei Quantil-Prognosemodellen.
Weitere Informationen
- Sequential Quantile Prediction of Time Series, March 2011, by Gerard Biau and Benoit Patra, Information Theory, IEEE Transactions
- Continuous Ranked Probability Score (CRPS), eine Verallgemeinerung der Pinball-Loss-Funktion für probabilistische Vorhersagen
