von Joannès Vermorel, Februar 2012Die Quantil-Regression ist eine Art der Regression (d. h. Prognose), die
absichtlich eine Verzerrung des Ergebnisses herbeiführt. Anstelle den
Durchschnittswert der Variablen vorherzusagen, befasst sich die Quantil-Regression mit dem
Mittelwert und anderen Quantilen (auch
Perzentile genannt). Quantile sind besonders
nützlich bei der Lagerbestandsoptimierung, als eine direkte Methode zur Berechnung des
Reorder-Points.
Regression ist hier ein Synonym für Prognose. "Regression" hebt den mathematischen Ansatz hervor, während "Prognose" die praktische Verwendung des Ergebnisses unterstreicht.
Der Begriff Quantil-Regression ist ein äußerst fortgeschrittenes statistisches Thema. Ziel dieses Artikel ist nicht die ausführliche Behandlung dieses Themas, sondern eine (ziemlich) intuitive Einführung in das Thema für Praktizierende aus dem Einzelhandel und der Herstellung.
Bildliche Darstellung von Quantilen
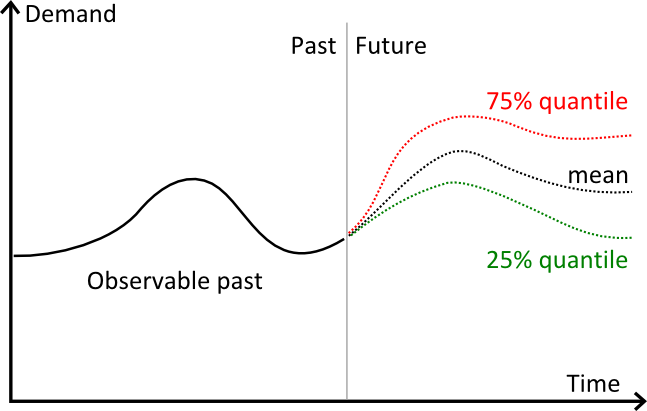
Das Diagramm oben zeigt 3 bestimmte Prognosen an:
- rot: 75% Quantil-Prognose
- schwarz: Durchschnittsprognose
- grün: 25% Quantil-Prognose
Optisch betrachtet verhalten sich Quantile wie Konfidenzintervalle. In der Praxis werden Quantile jedoch nur für einen einzigen Zielprozentsatz benötigt.
Quantile (oder Perzentiele) der zukünftigen Nachfrage
Die klassische und intuitivste Prognoseart ist die
Durchschnittsprognose: Überprognosen und Unterprognosen sollten sich die
Balance halten, ansonsten wäre die Prognosse
verzerrt (präziser geagt:
voreingenommen gegen).
Obwohl eine unvorbelastete Prognose wünschenswert ist, lässt dies noch lange nicht auf die Genauigkeit der Prognose schließen. Eine Prognose kann sowohl unvorbelastet als auch äußerst unkorrekt sein. Die Verzerrung bezieht sich lediglich auf den Teil des Prognosemodells zur Über- bzw. Unterprognostizierung der Zukunft.
Eine erste Verfeinerung dieser Vision ist die
Durchschnittsprognose: die jeweilige
Häufigkeit der Über- und Unterprognosen sollte sich die Waage halten, da sonst die Prognosen
gegenüber der Durchschnittsprognose parteiisch wären.
Nun haben wir den Begriff
unverzerrter Prognosen von
gleichen Gewichtungen hin zu
gleichen Vorteilen bewegt. Dieser Veränderung ist zwar nur gering, kann in manchen Situationen jedoch große numerische Auswirkungen haben.
Illustration: Durchschnitts- vs Medianeinkommen in den USA
Das
Haushaltseinkommen illustriert den tiefgreifenden Unterschied zwischen Durchschnitt und Median.
Laut der amerikanischen Statistikbehörde betrug das Median-Haushaltseinkommen im Jahr 2004 $44.389, während im gleichen Jahr das Durchschnittseinkommen $60.528 betrug - das sind fast 40% mehr als der Medianwert.
Diese Diskrepanz lässt sich durch (vergleichsweise) hohe Einkommen der reichsten US-Haushalte im Vergleich zum Rest der Nation erklären. Solche Unterschieden zwischen Durchschnitts- und Medianwert können in allen Verteilungen gefunden werden, die nicht symmetrisch sind. Im Regelfall handelt es sich um alle Verteilungen die keiner Normalverteilung entsprechen.
Verallgemeinerung des Median
Der Median repräsentiert die Schwelle an der die Verteilung in 50/50 Quoten unterteilt wird. Es ist jedoch möglich
andere Frequenzquoten in Betracht zu ziehen. Beispielsweise: 80/20 oder 90/10. Die Gesamtsumme muss immer 100% ergeben.
Quantile repräsentieren eine
die Verallgemeinerung des Median zu einem bestimmten Prozentsatz. Für τ, ein Wert zwischen 0 und 1, repräsentiert die Quantil-Regression Q(τ) den Schwellpunkt, an dem die Wahrscheinlichkeit einen Wert niedriger als den Schwellwert zu beobachten, exakt τ beträgt.
Quantil-Prognosen
Sowhl klassische als auch Quantil-Prognosen benötigen
Zeitreihen als Eingabedaten. Die Zeitreihen repräsentieren die Eingangsdaten. Zusätzlich zu diesen Daten, benötigt eine klassische
Durchschnittsprognose zwei weitere Struktureinstellugnen:
- den Zeitraum, z. B. Tag, Woche, Monat
- den Horizont, eine ganze Zahl, die die Anzahl der zu prognostizierenden Perioden darstellt
Die Zeitreihen werden entsprechend dem
Zeitraum angesammelt und der Horizont wird, um von praktischem Nutzen zu sein, entsprechend groß, und zwar meistens größer als die
Durchlaufzeit ausgewählt.
Durchschnittsprognosen profitieren davon: es ist
mathematisch korrekt, die Prognosen zusammenzufassen. Z. B., wenn
y1,
y2,
y3 und
y4 die Prognose für die nächsten vier Wochen repräsentieren, können wir, wenn wir
ausschließlich die zu erwartende Nachfrage für die nächsten
zwei Wochen benötigen, folgendes zusammenfassen:
y1+y2.
Die
Zusammenfassung von Quantil-Prognosen ist jedoch mathematisch inkorrekt, bzw. genauer gesagt, die Summe der Quantile entspricht nicht dem Quantil der Summe (Summe der einzelnen Segmente).
Lassen Sie uns erklären, warum Quantile nicht zusammegefasst werden können. Gehen wir von einem Glücksspieler aus, der jede Woche $1 in eine Spielautomaten wirft. Es wird angenommen, dass die Gewinnchangen bei einem Prozentsatz von 1% für einen Preis von $50 und sonst bei Null liegen. Nimmt man nun die 99% Wahrscheinlichkeit (Quantil) des zu erwartenden Gewinns, ergibt sich ein wöchentlicher Preis von $50 pro Woche. Nimmt man jedoch die 99% Wahrscheinlichkeit (Quantil) über zwei Wochen, beträgt der zu erwartende Gewinn immer noch $50. Tatsächlich liegt die Wahrscheinlichkeit zweimal zu gewinnen bei lediglich 0,01% (1% multipliziert mit 1%), von daher bleibt die Wahrscheinlichkeit von 99% unverändert. Summiert man die zwei Quantile von 99% erhält man $100. In der Realität dauert es jedoch 16 Wochen, um $100 Gewinn aus der 99% Wahrscheinlichkeit zu erzielen (einen Nachweis für dieses numerische Ergebnis wurde aus Platzgründen nicht eingefügt).
Da Quantil-Prognosen nicht zusammengefasst werden können, müssen Quantil-Zeitreihen-Prognosen den
Begriff der Zeitraum-Zusammenfassung neu überdenken. Die Erstellung von Quantil-Prognosen
pro Zeitraum ist fraglich, da diese
elementaren Prognosen nicht zusammengefasst werden können, um korrekte Quantile über bestimmte Zeitabschnitte zu erstellen.
Von daher verfügt die
Quantil--Zeitreihen-Prognose über eine bestimmte Struktur:
- τ der geplante Quantil, ein Prozentsatz.
- λ der Horizont, ein Zeitraum (im Regelfall: Tage).
Beispielsweise, wenn die Zeitreihen den Verkauf eines Produkts A, mit den Einstellungen τ=0,90 und λ=14 Tage, repräsentieren, dann wird die Quantilprognose (τ, λ) den Nachfragewert liefern, dessen exakte Wahrscheinlichkeit größer zu sein als die Gesamtnachfrage der letzten 14 Tage, 90% beträgt. (dementsprechend entspricht dies einer 10%-ige Chance niedriger zu sein als die Gesamtnachfrage der letzten 14 Tage).
Im Gegensatz zu klassichen Prognosen, produzieren Quantil-Prognosen unabhängig vom Horizont
einen und wirklich nur eine Wert pro Zeitreihe. Zu einem gewissen Grad sind Quantil-Prognosen
Zeitraum-agnositischer als deren Gegenstück.
Lokad hat die Lösung
Auf den ersten Blick erscheinen Quantil-Prognosen komplizierter als die klassische Version. In der Praxis jedoch, werden zuerst
Durchschnittsprognosen erstellt, um diese unverzüglich als Quantil-Prognosen zu
extrapolieren. Normalerweise wird davon ausgegangen, dass die Prognosen einer Normalverteilung entsprechen. Extrapolation stellt jedoch häufig das schwächste Glied im Prozess dar und kann das Endergebnis verfälschen. Die Prognosetechnologie sollte sich an die Praxisanforderungen anpassen, d. h. native Quantil-Prognosen und nicht anders herum.
Weitere Informationen
- Reorder-Point - Quantile und Lagerbestandsoptimierung.
- Pinball-Loss-Funktion - Genauigkeitsbewertung einer Quantil-Prognose.
- Roger Koenker, Kevin F. Hallock, (2001) Quantile Regression, Journal of Economic Perspectives, 15 (4), 143–156
- Ichiro Takeuchi, Quoc V. Le, Timothy D. Sears, Alexander J. Smola, (2006), Nonparametric Quantile Estimation, Journal of Machine Learning Research 7 1231–1264
