Von Joannès Vermorel, Dezember 2007 (zuletzt geändert, Januar 2012)Sicherheitsbestände stellen eine Methode für Bestandsoptimierung dar, bei der angezeigt wird, wie viel Bestand beim erwarteten Bedarf erforderlich ist, um ein bestimmtes Servicelevel zu erreichen. Der zusätzliche Bestand dient als „Sicherheitspuffer“ – daher auch der Name – und soll das Unternehmen vor erwarteten künftige Fluktuationen schützen. Die Formel für den Sicherheitsbestand hängt sowohl vom erwarteten künftigen Bedarf als von der erwarteten künftigen Durchlaufzeit ab. Es wird davon ausgegangen, dass die Ungewissheit für beide Faktoren normalverteilt ist. Die Formel für Sicherheitsbestände ist in den meisten Bestandsführungssystemen, insbesondere in ERPs und MRPs, zu finden.
Update Juli 2020: Der unten aufgeführte Ansatz ist ein Klassiker aus Supply-Chain-Lehrbüchern, der leider auch dysfunktional ist. Hervorzuheben ist, dass weder der künftige Bedarf noch die künftige Durchlaufzeit normalverteilt sind (d.h., sie sind keine Gaußglocken). Zusätzlich ignoriert dieser Ansatz komplett, dass alle SKUs, die vom Unternehmen bestellt oder hergestellt werden können, um dieselben Ressourcen konkurrieren. Deshalb empfehlen wir mit Nachdruck, das Modell der Sicherheitsbestände nicht in echten Supply-Chains einzusetzen.
Angedachte Zielgruppe: Dieses Dokument ist primär für Fachleute im Lieferantenmanagement, im Einzelhandel oder der Fertigung, bestimmt. Dennoch kann dieses Dokument auch für Softwareentwickler in den Bereichen Buchhaltung/Warenwirtschaft/E-Commerce sinnvoll sein, die Ihre Anwendungen um Funktionalitäten der Bestandsverwaltung erweitern möchten.
Auch wenn wir versucht haben die mathematischen Voraussetzungen so gering wie möglich zu halten, können wir insgesamt jedoch nicht alle Formeln vermeiden, da der eigentliche Zweck dieses Dokumentes in einem praxisnahen Leitfaden besteht, der erklärt wie man Sicherheitsbestände berechnet.
Herunterladen: Berechnung-Sicherheitsbestände.xls (Microsoft Excel Tabelle)
Einleitung
Die Bestandsverwaltung ist eine
finanzielle Abwägung zwischen Bestandskosten und Fehlmengenkosten. Je mehr Bestand, desto mehr Nettoumlaufvermögen wird benötigt und desto mehr Bestandswertminderung müssen Sie in Kauf nehmen. Auf der anderen Seite, wenn Sie über einen unzureichenden Bestand verfügen, kann dies zu Inventur Bestandsfehlmengen, potentiellen Umsatzeinbußen und der Möglichkeit der Unterbrechung des gesamten Fertigungsprozesses führen.
Der Inventurbestand hängt grundsätzlich von zwei Faktoren ab;
- Leitnachfrage: die Anzahl der Güter, die konsumiert oder gekauft werden
- Beschaffungszeit: die Verzögerung zwischen der Neubestellung und der erneuten Verfügbarkeit
Diese beiden Faktoren unterliegen jedoch Unsicherheiten;
- Nachfrageschwankungen: Kundenverhalten kann sich auf recht unvorhersehbare Weise verändern
- Beschaffungszeitschwankungen: Lieferanten oder Transportunternehmen können ungeplanten Schwierigkeiten gegenüberstehen
Die Entscheidung über die Höhe des Sicherheitsbestandes impliziert eine Abwägung zwischen diesen Kosten und den Unsicherheiten.
Die Balance zwischen Bestandskosten und Fehlmengenkosten, hängt stark vom Geschäft ab. Anstatt daher diese Kosten direkt zu berücksichtigen, wollen wir die klassische Idee des
Service-Level einführen.
Der
Service-Level drückt die Wahrscheinlichkeit aus, dass eine bestimmte Höhe an Sicherheitsbestand nicht zu einer Ressourcenknappheit führen wird. Selbstredend führt der Anstieg des Sicherheitsbestandes auch zu einer Erhöhung der Dienstgüte. Ist der Sicherheitsbestand sehr hoch, tendiert die Dienstgüte gegen 100% (z.B. eine Wahrscheinlichkeit von Null bezüglich der Ressourcenknappheit).
Die Wahl der Dienstgüte, d. h. die Akzeptanzwahrscheinlichkeit eines Fehlbestands, sprengt den Rahmen dieses Leitfadens. Weitere Informationen hierzu finden Sie in unserem Leitfaden
Kalkulation optimaler Service-LevelInventur-Wiederbeschaffungsmodell
Der Reorder-Point entspricht der Höhe des Bestandes, die eine Bestellung auslösen sollte. Wenn es wenige Unsicherheiten zu beachten gab (z.B. der zukünftige Bedarf genau bekannt war und Lieferungen absolut zuverlässig), wäre der Zeitpunkt der Nachbestellung gleich dem prognostizierten Gesamtbetrag während der Beschaffungszeit, auch
Bedarf an Beschaffungszeit genannt.
In Wirklichkeit haben wir aufgrund der Ungewissheiten:
Zeitpunkt der Nachbestellung = Bedarf an Beschaffungszeit + SicherheitsbestandUnter der Annahme, dass die Prognosen keine Verzerrung aufweisen, würde ein Sicherheitsbestand von 0 zu einer Dienstgüte von 50% führen. Erwartungstreue Prognosen bedeuten tatsächlich, dass eine Möglichkeit besteht, dass der zukünftige Bedarf höher oder niedriger als der Bedarf an Beschaffungszeit ist (nicht vergessen: der Bedarf an Beschaffungszeit ist lediglich ein prognostizierter Wert).
Vorsicht: Prognosen können erwartungstreu sein ohne gleichzeitig exakt zu sein. Eine Verzerrung weist auf einen systematischen Fehler im Prognosemodell hin (z.B. eine kontinuierliche Überschätzung des Bedarfs um 20%).
Normalverteilung des Fehlers
Zu diesem Zeitpunkt benötigen wir eine Art, die Unsicherheit des Bedarfs an Beschaffungszeit zu repräsentieren. Im Folgenden gehen davon aus, dass der Fehler normalverteilt ist (siehe Graphik weiter unten).
 Statistische Anmerkungen
Statistische Anmerkungen: die Annahme einer Normalverteilung ist nicht vollends willkürlich. Unter bestimmten Bedingungen, nähern sich statistische Schätzwerte, wie in dem zentralem Grenzwertsatz skizziert, einer Normalverteilung an. Aber derlei Überlegungen sprengen den Rahmen dieses Leitfadens.
Eine Normalverteilung ist durch lediglich zwei Parameter definiert: ihren Erwartungswert und ihre Varianz. Da wir eine erwartungstreue Prognose erwarten, nehmen wir an, dass der Erwartungswert der Fehlerverteilung Null sein wird. Dies bedeutet nicht, dass wir keinen Fehler annehmen.
Die Festlegung der Varianz des Prognosefehlers ist eine heiklere Aufgabe. Lokad bietet wie die meisten Vorhersagewerkzeug, verknüpft mit seinen Prognosen,
MAPE-Schätzungen (
Mean
Absolute
Percentage
Error - Prozentsatz des absoluten Fehlers des Erwartungswertes). Der Vollständigkeit halber, möchten wir erklären, wie bloße Heuristiken genutzt werden können, um dieses Problem zu überwinden.
Im Einzelnen kann die
Varianz innerhalb der historischen Daten als geeignete Heuristik zur Schätzung der Prognose der Fehlervarianz genutzt werden. David Piasecki schlägt vor, anstelle des mittleren Bedarfs in der Varianzformel, den prognostizierten Bedarf zu benutzen. Dementsprechend ist:
σ2 = E[ (yt - y')2 ]
wobei
E der E
rwartungswert-Operator ,
yt der historische Bedarf für den Zeitraum
t (typischerweise die Höhe des Absatzes) und
y' der prognostizierte Bedarf ist.
Die Schlüsselidee, die hinter dieser Annahme steckt, ist, dass der Prognosefehler oft mit der erwarteten Varianz korreliert:
Je höher die auftretende Varianz, desto höher der Fehler in der Prognose.
Die Berechnung dieser Fehlervarianz beinhaltet tatsächlich einige Feinheiten, die weiter unten ausführlicher behandelt werden.
Formel für den Sicherheitsbestand
Bis jetzt haben wir sowohl den Erwartungswert wie auch die Varianz bestimmt, daher ist die Fehlerverteilung bekannt. Nun müssen wir das akzeptiere
Fehlerniveau innerhalb dieser Verteilung berechnen. Weiter oben haben wir die Idee der Dienstgüte (ein Prozentsatz) eingeführt, um dies zu bewerkstelligen.
Anmerkungen: Wir gehen von einer statischen Beschaffungszeit aus. Dennoch kann auch für eine dynamische Beschaffungszeit ein ähnlicher Ansatz genutzt werden. Siehe auch
Um die Dienstgüte in ein
Fehlerniveau umzuwandeln, auch
Service Faktor genannt, müssen wir die
kumulierte Normalverteilung (manchmal auch umgekehrte Normalverteilung genannt) betrachten. Auch wenn dies vielleicht kompliziert erscheint - dem ist nicht so. Wir schlagen vor, einen kurzen Blick auf die
Minianwendung zur Normalverteilung zu werfen, um einen mehr visuellen Eindruck zu erhalten. Wie Sie sehen können, transformiert die kumulierte Funktion den Prozentsatz in einen
Bereich-unterhalb-der-Verteilung, die X-Achsenschwelle korrespondiert mit dem Wert des Service Faktor.
Intuitiv berechnen wir
Sicherheitsbedarf = Standardabweichung des Fehlers * Service FaktorFormaler, mit
S als Sicherheitsbestand, haben wir
S = σ * cdf(P)
wobei
σ die Standardabweichung (z.B. Quadratwurzel von
σ2 die oben definierte Varianz),
cdf die
normalisierte kumulierte Normalverteilung (Null als Erwartungswert und die Varianz gleich eins) und
P die Dienstgüte ist.
Erinnern Sie sich, dass
Zeitpunkt der Nachbestellung = Bedarf an Beschaffungszeit + Sicherheitsbestand
Mit
R als Zeitpunkt der Nachbestellung, haben wir
R = y' + σ * cdf(P)Abgleich zwischen Beschaffungszeit und Prognosezeitraum
Bisher haben wir schlichtweg angenommen, dass wir für die
Beschaffungszeit eine direkt korrespondierende, zukünftige Bedarfsprognose erstellen können. In der Praxis funktioniert dies nicht zwangsläufig so. Die
Analyse der historischen Daten beginnt meist mit der Anhäufung der Daten in Zeitabschnitte (meist wöchentlich oder monatlich).
Dennoch kann es vorkommen, dass der ausgewählte Zeitraum nicht hundertprozentig mit der Durchlaufzeit übereinstimmt. Somit sind zusätzliche Berechnungen erforderlich, um die Leitnachfrage und die damit verbundenen Abweichungen auszudrücken (vorausgesetzt wir gehen immer noch davon aus, dass eine normale Verteilung des Prognosefehlers vorliegt; siehe vorangehender Abschnitt).
Der
Bedarf an Beschaffungszeit kann intuitiv als Summe der prognostizierten Werte der zukünftigen Zeiträume, die sich mit dem Segment der Beschaffungszeit schneiden, berechnet werden. Der letzte Prognosezeitraum sollte sorgfältig angepasst werden.
Formal sei
T der Zeitraum und
L die Beschaffungszeit. Wir schreiben
L = k * T + α * T
mit
k integer und
0 ≤ α < 1.
D wird als Bedarf der Beschaffungszeit definiert. Dann haben wir noch die letzte Formel für den Bedarf an Beschaffungszeit
D = (Σt=1..k y't) + αy'k+1
mit
y'n als prognostiziertem Bedarf für
nth Zeitraum in der Zukunft.
Unter denselben Annahmen bezüglich der Normalverteilung, können wir die Varianz des Prognosefehlers, wie folgt berechnen:
σ2 = E[ (yt - y')2 ]
mit
y' als durchschnittliche Prognose pro Zeitraum
y'= D / (k + α)σ2 wird hier dennoch als
pro-Zeitraum Varianz berechnet, obwohl wir eine Varianz bräuchten, die stattdessen die Beschaffungszeit abbildet. Sei
σL2 die angepasste pro-Beschaffungszeit Varianz, erhalten wir:
σL2 = (k + α) σ2Schließlich, können wir den Zeitpunkt der Nachbestellung umformulieren zu:
R = D + σL * cdf(P)Die Nutzung von Excel zur Berechnung des Zeitpunktes der Nachbestellung
In diesem Abschnitt wird dargestellt,
wie man den Zeitpunkt der Nachbestellung mit Microsoft Excel berechnet. Zum besseren Verständnis empfehlen wir einen Blick auf die oben dargestellte
Beispiel Excel-Tabelle zu werfen.
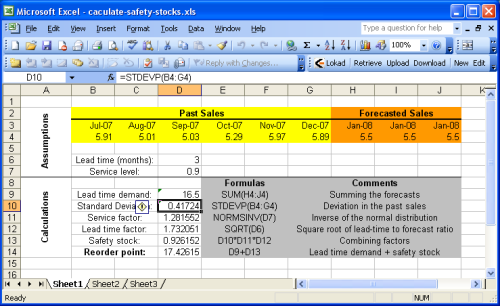
Die Beispiel Tabelle ist grundsätzlich in zwei Abschnitte aufgeteilt: Die
Annahmen oben und die
Berechnungen unten. Die Prognosen werden als Teil der Annahmen aufgefasst, da eine Erläuterung der Verkaufs- (oder Bedarfs-) prognose, den Rahmen dieses Leitfadens sprengen würde. Bitte beziehen Sie sich für Details auf die
Tutorials zur Verkaufsprognose mit Microsoft Excel.
Die meisten der im vorherigen Abschnitt eingeführten Formeln, sind einfache Operationen (Addition, Multiplikation), die einfach in Microsoft Excel durchgeführt werden können. Dennoch möchte ich die Aufmerksamkeit auf zwei Formeln lenken:
NORMSINV (Microsoft KB): schätzt die kumulierte Normalverteilung ab, oben als cdf bezeichnet.STDEV (Microsoft KB): schätzt die Standardabweichung ab, hier mit σ bezeichnet. Wir erinnern uns, dass die Standardabweichung σ die Quadratwurzel der Varianz ist σ2.
Der Einfachheit halber, führt die erste Tabelle die Heuristik
σ2 = E[ (yt - y')2 ] bei der Berechnung des Service Faktors, nicht ein. Dieser Ansatz wird erst in
Sheet2 (zweite Tabelle des Excel-Dokumentes) eingeführt. Da wir bei der Prognose von statischen Prognosen ausgehen, bleibt der Zeitpunkt der Nachbestellung, mit oder ohne Heuristik, gleich.
Ressourcen
inventoryops.com: großartige online Ressource von David J. Piasecki, Autor des Buches
Inventory Accuracy: People, Processes, & Technology.

